гомерных систем часто вместо условий Рауса - Гурвица используют критерий Найквиста. Однако, так как в настоящей книге рассматриваются только системы двух дифференциальных уравнений, для которых характеристическое уравнение является квадратным уравнением, то мы здесь не обращаемся к этим общим критериям.

Исследование вопроса о том, при каких значениях параметров, входящих в правые части динамических систем, рассматриваемое состояние равновесия устойчиво, позволяет выделить область устойчивости этого состояния равновесия в пространстве параметров. Мы будем дальще называть эту область областью Рауса - Гурвица.

Хотя основной интерес для прикладных вопросов (в которых играет роль устойчивость равновесных режимов) имеют такие системы, действительные части корней характеристических уравнений которых отрицательны, т. е. системы со значениями параметров внутри области Рауса - Гурвица, тем не менее для ряда прикладных вопросов представляет интерес выяснение поведения системы в случае, когда изображающая ее в пространстве параметров точка лежит на границе области Рауса - Гурвица или (что физически эквивалентно) достаточно близко к этой границе. Дело в том, что в прикладных вопросах приходится считаться не только с требованиями устойчивости, но и с другими требованиями, относящимися к работе устройства, и мон<ст оказаться, что одновременное удовлетворение этих условий наилучщим образом достигается выбором параметров, соответствующих точкам, лежащим в сравнительной близости к границам области Рауса - Гурвица. Таким образом, возникает вопрос о поведении динамической системы вблизи границы области Рауса - Гурвица. Действительно, выбирая значения параметров, близкие к границе этой области, мы никогда не можем быть уверены, что случайные отклонения этпх параметров в реальной системе не выведут точку, представляющую систему в пространстве параметров, за границу области Рауса - Гурвица.

Поведение динамической системы при малых отклонениях от границы области Рауса - Гурвица определяет и особенности поведения систем, для которых представляющая их точка в пространстве параметров лежит в области Рауса - Гурвица, но в достаточной близости к границам этой области.

Как мы видели в предыдущем параграфе, вопрос о повсде-пии системы в случае, когда изображающая ее точка в пространстве параметров переходит через границу области Рауса - Гурвица (именно, через границу, соответствующую системе со сложным фокусом), связан с вопросом возбуждения колебаний (мягкого и жесткого самовозбуждений, см. § 3).

Мы рассмотрим сначала те точки границы области Рауса - Гурвица, которые соответствуют негрубым состояниям равновесия первой степени негрубости - именно, сложному фокусу с

не равной нулю первой ляпуновской величиной (коэффициент аз в функции последования) и двукратному состоянию равновесия - седло-узлу.

В этом случае части границы области Рауса - Гурвица могут быть двоякой природы: безопасные границы - достаточно малое нарушение которых влечет за собой лишь весьма малые (сколь угодно малые при достаточно малых нарушениях) изменения состояния системы; опасные границы - сколь угодно малое нарушение которых повлечет за собой переход системы в новое состояние, которое мы не можем приблизить к исходному выбором достаточно малых нарушений границы.

Иначе говоря, может оказаться, что состояние равновесия измененной системы (сколь угодно мало измененной) будет неустойчиво, но практически система будет вести себя как устойчивая, так как изображаюш;ая точка, взятая из некоторой окрестности состояния равновесия, будет для всех t (начиная с начального значения о) оставаться в малой окрестности состояния равновесия (сколь угодно малой при достаточно малых изменениях системы), и, наоборот, может оказаться, что, хотя состояние равновесия измененной системы устойчиво, но система практически будет неустойчива, так как изображающую точку, взятую вне малой окрестности состояния равновесия (сколь угодно малой при достаточно малых изменениях системы), нельзя заставить оставаться вблизи состояния равновесия.

Предположим, что рассматриваемое состояние равновесия лежит в начале координат, так что мы можем предполагать систему в виде

х = а{},)х + Ь{К)у + Р{х, у, Я), yc{},)x + d{K)y + Qix, у, Я),

где Я - параметр.

Рассмотрим подробно два указанных выше случая поведения системы при значениях Я, близких к значению Яо, соответствующему сложному фокусу пли седло-узлу первой степени негрубости (см. гл. 10).

I. При Я = Яо система имеет сложный фокус первого порядка, т. е. состояние равновесия с чисто мнимыми характеристическими корнями, у которого первая ляпуновская величина Li = = аз(?ц)) отлична от нуля. Вводя обозначения

А(Я) = а(Я)й(Я)-Ь(Я)с(Я), Л(Я)= а(Я)+ й(Я)

(Д(Я)/2 - действительная часть характеристических корней), мы, очевидно, будем иметь в рассматриваемом случае Л(Яо)>0, Л(Яэ)-0.

Далее естественно сделать предположение, что дН/дКФО. Мы получим наглядную картину поведения системы вблизи гра-15*

ницы области устойчивости, рассматривая изменение качественной структуры в окрестности состояния равновесия в зависимости от изменения параметра К. Как мы видели (см. гл. И), возможны следующие случаи:

а) Ll < О, сложный фокус устойчив. При переходе через границу R{K) = 0 от значений К<Ко к значениям КЖо появляется единственный устойчивый предельный цикл. При обратном изменении параметра Я. устойчивый цикл стягивается в точку (в сложный фокус);

б) Ll > О, сложный фокус неустойчив. При переходе через границу R(K)=0 от значений Я < Яо к значениям Я > Яо к состоянию равновесия стягивается единственный неустойчивый) предельный цикл; при обратном изменении параметра из состояния равновесия появляется неустойчивый предельный цикл.

Изменение качественной структуры разбиения окрестности состояния равновесия на траектории для этпх двух случаев изображено на рис. 117, 118. Штриховкой показана область

Случаи lf</J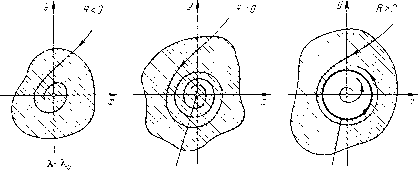

Сложный 0OhjC

Рис. 117

Успоичидый предельный цикл А>Л

устойчивости, для которой траектории представляют собой спирали, накручивающиеся на состояние равновесия, или предельный цикл. Область неустойчивости заполнена раскручивающимися спиралями. Рисунки наглядно показывают различие в поведении системы вблизи границы по отношению к случайным толчкам. Сравнивая для й < О случаи Li < О и Li > О, видим, что во втором случае возможно выбивание случайным толчком изображающей точки из устойчивого состояния равновесия за границы области устойчивости (внутри рассматриваемой окрестности состояния равновесия), тогда как в первом случае это