невозможно. Рисунки показывают, далее, различие в поведении системы при нарушении условий устойчивости. Переход через границу й = О в первом случае {Li < 0) соответствует возникновению области неустойчивости внутри устойчивого предельного цикла, которая, однако, остается сколь угодно малой при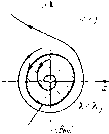

еустоа предельный цинл

иГО>кньш фонде 6

Рпс. 118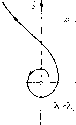

достаточно малом нарушении условии устойчивости и стягивается в точку при обратном изменении параметра; изображающая точка при этом возвращается в состояние равновесия - система ведет себя обратимо. Во втором случае {L\ > 0) переход через границу й = О соответствует исчезновению области устойчивости внутри неустойчивого предельного цикла; изображающая точка при этом срывается с состояния равновесия и уходит за пределы рассматриваемой окрестности состояния равновесия. При обратном изменении параметра изображающая точка не возвращается в состояние равновесия - система ведет себя необратимо.

В § 3 настоящей главы при рассмотрении жесткого возникновения колебаний изображающая точка после срыва уходит на устойчивый предельный цикл, окружающий начало, в силу предположения о специальном характере разбиения плоскости на траектории. Однако при другом виде фазовой плоскости изображающая точка после срыва при Я = Яо может пойти либо к другому устойчивому состоянию равновесия, либо к предельному циклу, не окружающему начало. Мы вернемся к этому более сложному случаю в следующем параграфе.

П. При Я = Яо система имеет двукратное состояние равновесия - седло-узел, т. е. состояние равновесия, для которого

Л(Яо)=0 и а(Яо)+й(Яо)<0, /(Яо)=0 (неравенство нулю /(Яо) и означает, что точка двукратная).

Состояние равновесия О (см. гл. 4, 9, 10) имеет вид, представленный на рис. 119,6). Вблизи границы А(Я) = 0 малая окрестность состояния равновесия О имеет вид, представленный на одном из рис. 119. Из рисунков видно, как при приближении к границе А(Я)=0 в малую окрестность устойчивого состояния равновесия вторгается область неустойчивости (на рис. 119, я, я, б заштрихованная область), попав в которую изо-бражаюп];ая точка выбрасывается из рассматриваемой окрестности состояния равновесия. Для изображаюп];ей точки ири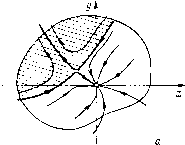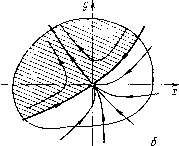

Рис. 119

приближении к границе А(Я)=0 возрастает опасносЯь быть выброшенной случайным толчком из устойчивого состояния равновесия. При невырожденном вхождении параметра Я, при его изменении от значений Я < Яо к значениям Я > Яо мы получаем последовательность качественных структур, изображенных на рис. 119.

Значениям Я < Яо соответствуют рис. 119, я и 119, я (два состояния равновесия - узел и седло), значению Я = Яо - рис. 119,6 (начало координат - седло-узел), значениям Я > Яо - рис. 119, в (сложное состояние равновесия-седло-узел исчезает).

Рассмотренная граница области устойчивости, очевидно, является опасной.

После исчезновения седло-узла изображающая точка либо стремится к устойчивому состоянию равновесия или к устойчивому предельному циклу, близкому к тому, к которому стремилась а-сепаратриса седло-узла (см. рис. 103 гл. 10), либо, в случае, когда сепаратриса седло-узла возвращается в него же, начинает двигаться (сначала с очень большим периодом) по предельному циклу, образовавшемуся из сепаратрисы седло-узла (см. рис. 104 гл. 10). Во всех этих случаях граница области устойчивости опасна.

Следует, однако, обратить внимание на то, что если при значениях К <ко изображающая точка двигается по предельному циклу, на котором при К = Ко возникает двукратное состояние равновесия седло-узел, то соответствующая граница, очевидно, является безопасной (изображающая точка не выходит из окрестности цикла).

Рассмотрим еще дополнительно поведение динамических систем вблизи тех точек границы, в которых А > О и й = О, где безопасная граница переходит в опасную, т. е. где первая ляпуновская величина L\ обращается в нуль. В этом случае поведение системы может быть определено знаком второй ляпуновской величины L2 = 0,50 (см. гл. И, § 5).

При рассмотрении этого случая мы предположим, что в систему входит не один, а два параметра Я и л (при наличии только одного параметра картина смазывается), и пусть в некоторой точке М(Яо, ро) плоскости параметров й=0, Li = О, но ЬгФО. На рис. 120 большая точка соответствует точке плоскости параметров, в которой й = О, Li = О, 2 =5 0; в точках части линии й = О, обозначенной белыми точками, Li>0 (для соответствующих значений параметров система имеет неустойчивый сложный фокус первого порядка); в точках частп линии й = О, обозначенной черными точками, Li <0 (система имеет устойчивый сложный фокус).

В заштрихованной части плоскости параметров й < О, в не-заштрихованной (но в которой может быть область, обозначенная мелкими штрихами) й > 0. Напомним, что при переходе через часть границы й = О, в которой Li < О, из заштрихованной области в незаштрихованную из сложного фокуса рождается устойчивый предельный цикл, а при переходе через й = О, где Li > О, из незаштрпхованной в заштрихованную область - неустойчивый цикл.

Пусть в точке, в которой R = Li = О, мы имеем L2 > О, тогда соответствующий сложный фокус (второй степени негрубо-;ти) неустойчив (рис. 120, а, 121, й).

Если в пространстве параметров мы перейдем по линии Й = 0 в точки, где Li<0, то, как нетрудно показать, рассмат-