венную структуру, но и получить также некоторые количественные характеристики.

Следует, однако, заметить, что полное рассмотрение кусочно-сшитых систем методом точечных преобразований, как правило, в основном возможно лишь в случае, когда частные системы, из которых система склеена, являются линейными (т. е. именно в случае, когда система кусочно-линейная). Между тем далеко не всегда, исходя из условий реальной задачи, естественно рассматривать кусочно-линейную систему, для некоторых задач естественно рассматривать системы, склеенные из нелинейных и неинтегрируемых динамических систем. В этом случае исследование системы методом точечных преобразований не может быть проведено.

Кроме того, следует принять во внимание также следующее: целесообразность введения и рассмотрения кусочно-склеенных систем может быть вызвана не только - если так можно выразиться - физическими причинами, т. е. тем, что физические свойства рассматриваемой системы хорошо описываются склеенными системами (например, как в указанных выше простейших примерах), но также п математическими причинами. Именно, иногда для упрощения математического исследования некоторые функции, характеризующие рассматриваемую реальную систему, заменяются кусочно-сшитыми функциями (до написания системы дифференциальных уравнений или после ее написания).

Так, например, в некоторых случаях функция I/ = sin ф (см. рис. 184,а) заменяется либо непрерывной кусочно-склеенной функцией, представленной на рис. 184,6, либо даже разрывной функцией, представленной на рис. 184, в. Теоретически всякая система может быть приближенно представлена как склеенная из достаточно большого числа линейных систем, так как в достаточно малой области всякая система может быть приближенно представлена как линейная. Однако использование этого весьма общего утверждения при рассмотрении конкретных задач, вообще говоря, не представляется возможным из-за его полной неэффективности.

Если ири рассмотрении конкретной задачи делается такая замена аналитических функций кусочно-сшитыми (или даже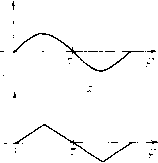

Рис. 184

разрывными), то, очевидно, сразу же встает вопрос, будет ли полученная кусочно-сшитая система (введенная из математических соображений) правильно отражать те черты реальной системы, которые должны описываться не склеенной аналитической системой.

Этот вопрос подлежит детальному обсуждению, и ему посвя-ш;ена гл. 20 настояш;ей книги.

Так или иначе, в силу ли физических или математических причин возникает целесообразность рассмотрения кусочно-сшитых, но не обязательно кусочно-линейных (и даже не обязательно кусочно-интегрируемых) динамических систем и их качественного исследования. Но в случае, когда сшитая система не является кусочно-линейной, полное сведение исследования ее качественной структуры к исследованию некоторого точечного отображения, как правило, делается невозможным. Тогда естественно попытаться распространить теорию бифуркаций и методы качественного исследования, на нее опираюш;иеся, на кусочно-сшитые системы, конечно, с той спецификой, которая при этом возникает. Это тем более естественно, что в случае кусочно-сшитых систем, так же как и в случае аналитических систем, фактами теории бифуркаций объясняются некоторые черты поведения реальных систем (мягкое и жесткое возникновение колебаний, срыв колебаний и др.).

В настояи];ей книге при качественном рассмотрении сшитых систем используется не только построение функции последования (точечного отображения) и его исследование, но также и приемы, опираюш;иеся на перенесенную на сшитые системы теорию бифуркаций.

§ 1. Сшитые системы. Доопределение на линиях сшивания.

В настояи];ей главе мы дадим определение кусочно-сшитых систем и укажем некоторые их основные свойства.

Нри этом мы ни в какой мере не претендуем на полное описание всех возможных типов кусочно-сшитых систем и их свойств (что и вообш;е вряд ли имеет смысл), а выделяем лишь некоторые, наиболее часто встречаюш;иеся в прикладных задачах.

Система

x = P{x,y),y = Q{x, у), (А)

определенная в некоторой области G плоскости {х, у) (область может, в частности, совпадать со всей плоскостью {х, у)), называется сшитой системой (или кусочно-сшитой, или кусочно-склеенной системой), если:

1. Задано разделение области G на конечное число подобластей G\, G2, ..., Gn (га 2), границы которых состоят из конечного числа:

а) линий, уходяш;их в бесконечность (в частности прямых);

б) простых замкнутых кривых;

в) простых дуг Zi, ..., Im.

При этом подразумевается, что линии и простые замкнутые кривые не имеют общих точек, а простые дуги могут иметь общими с линиями, простыми замкнутыми кривыми и друг с другом только свои концы.

Линпи, замкнутые кривые и простые дуги предполагаются аналитическими, т. е. если x = (f{s), y = {s)-параметрические уравнения линии, замкнутой кривой, дуги I, то функции ф(5) и являются аналитическими функциями s.

Границы областей Gj {] = 1, ..., п) называются линиями сшивания (или линиями склейки).

2. В каждой частичной области Gj вместе с ее границей (т. е. в замкнутой области Gj) определена частичная аналитическая динамическая система

dxldt = Pj{x, у), dy!dt = Qj{x, у). (kj)

Точнее, система {kj) задана, и правые части ее являются однозначными аналитическими функциями в некоторой областп Н, целиком содержащей Gj-, система {kj) как бы «отрезана» вдоль границы Gj.

Таким образом, на всякой линии сшивания, общей для двух областей С,- и G, определена как система (А;), так и система (Aft). Однако данная сшитая система может быть определена на линии сшивания совсем особым образом (она может быть отлична и от системы (А,), и от системы (А)). В каждой внутренней точке любой области Gj склеенная система (А) совпадает с системой (Aj).

3. На границах областей Gj, т. е. на линиях сшивания, система (А) специально доопределяется (в зависимости от условий ТОЙ реальной задачи, которая описывается рассматриваемой сшитой системой).

Прп сделанных нами предположениях относительно аналитичности частичных систем (Aj) и аналитичности линий, входящих в границы областей {Gj), очевидно, справедливы следующие утверждения.

Всякая простая дуга I, входящая в границу какой-либо областп Gj (которая может быть либо частью уходящей в бесконечность граничной линии, либо дугой граничной замкнутой кривой):

1) может быть дугой без контакта для траекторий системы (Ai), определенной в области G,- (для которой она является граничной), но может не быть дугой без контакта для траекторий системы (Аа), определенной в отличной от Gj области (для которой I также является граничной дугой);

2) может иметь конечное число точек касания с траекториями системы (Ai);