
 |
|
Главная страница Приемы качественного исследования [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [ 77 ] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] ривая функцию последования (см. гл. 8, § 3), на фазовой плоскости из сложного фокуса второго порядка родится неустойчивый предельный цикл (грубый), а фокус делается негрубым устойчивым (рис. 121,6). Если затем в пространстве параметров Случай Li>D Слитй L?<D Опасная гпаница а R<0 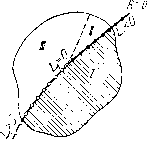 Рис. 120 Безопасная граница 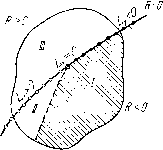 МЫ выйдем в незаштрихованную область (на рис. 120, а) область ), то из устойчивого сложного фокуса рождается устойчивый предельный цикл. При этом ранее родившийся неустойчи- Спучай L2>0 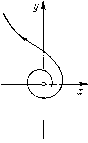 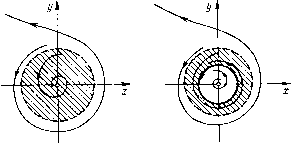 Неустойчибый предельный цикл Устойчивый и неустойчивый пребельные цикпы Рис. 121 вый цикл сохраняется, так что в области параметров 77 у системы на фазовой плоскости вокруг грубого неустойчивого фокуса будет существовать два предельных цикла (рис. 121, в). с другой стороны, нетрудно показать, что при значениях параметров в области / у системы вокруг неустойчивого фокуса нет предельных циклов. (При переходе из точки, где R = L\ = = 0, Z,2 > О, на часть линии Д == О, где Ly > О, циклы не рождаются, и в силу сделанных выше замечаний не рождаются при переходе в область /.) Но тогда при движении в пространстве параметров из области / в область непременно должны встретиться бифуркационные значения параметров, при которых у системы сугцествует двукратный цикл. На рис. 120 линия в пространстве параметров, соответствуюгцая двукратным предельным циклам, изображена штрихами. Аналогичное рассмотрение может быть проведено и в случае Z/2 < О (рис. 120, б и рис. 122, а - в). В рассмотренном случае знак второй ляпуновской величины L2 играет роль, подобную знаку L\, увеличивая или уменьшая 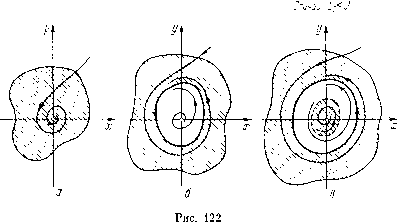 опасность для изображаюгцей точки быть выброшенной из окрестности состояния равновесия. Пусть 2 > О (при i? = Z/1 = 0) и пусть значения параметров достаточно близки к значениям, определяемым этими условиями; тогда в достаточно малой окрестности начала координат в фазовом пространстве может быть одна из структур, изображенных на рис. 121. При нарушении безопасной границы области устойчивости изображаюгцая точка остается в малой окрестности состояния равновесия вблизи устойчивого предельного цикла, если начальные возмущения не превосходят некоторой малой величины (определяемой размерами второго, неустойчивого предельного цикла, также вторгающегося в малую окрестность начала ко- 12) Напоминаем, что только в случае систем первой степени негрубости в окрестности точки границы области устойчивости в соответствующем функциональном пространстве негрубые системы образуют пленку. ординат); прп возмущениях, превосходящих эти пределы, изображающую точку нельзя заставить оставаться в малой окрестности состояния равновесия. С другой стороны, выбивание системы малым толчком пз устойчивого состояния равновесия возможно и вблизи безопасной границы области устойчивости (см. рис. 121). Пусть 2 < О (при R = Ll = 0), и пусть параметры опять мало изменены; тогда в достаточно малой окрестности начала координат может быть одна из структур, изображенных на рис. 122. Здесь даже нарушение опасной границы может оставить изображающую точку в малой окрестности состояния равновесия, если параметры достаточно близки к значениям, определяемым условиями R = Ll = 0. § 5. Замечания по поводу других гранпц области устойчивости. Мы рассмотрели части границы области устойчивости в случае, когда эти части соответствуют негрубым состояниям равновесия. Очевидно, аналогично могут быть рассмотрены границы области устойчивости, соответствующие еще и другим системам первой степени негрубости ); именно в нумерации § 6 гл. 9: 3) - системе, имеющей двукратный предельный цикл; 4)- системе, имеющей сепаратрису, идущую из седла в седло. Случай 3) естественным образом имеет место, когда при изменении параметра к устойчивому предельному циклу приближается неустойчивый предельный цикл (как в рассмотренном в § 3 случае жесткого возбуждения колебаний), который сливается с устойчивым циклом. Образуется двукратный цикл, который при дальнейшем изменении параметра исчезает. Изображающая точка «срывается» и стремится либо к устойчивому состоянию равновесия, либо к другому устойчивому предельному цик.чу. Граница опасная. Нетрудно убедиться, что система при любой ее качественной структуре в этом случае ведет себя необратимо. В случае 4) предположим, что изображающая точка при значениях Я <: Яо двигается по устойчивому предельному циклу, который при Я = Яо влипает в сепаратрису. Очевидно, по мере образования петли сепаратрисы период предельного цикла, влипающего в эту петлю, неограниченно увеличивается. Когда после образования петли петля разрушается без образования предельного цикла, что всегда имеет место при общем вхождении параметра, изображающая точка стремится к тому устойчивому [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [ 77 ] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] 0.0109 |