Откуда Из (4) имеем

= 3 1±1>0 (7)

du T)

Сравнивая (7) и (8), непосредственно обнаруживаем, что для любого т) будет

щуюся в точке (у, 0). «Сшивание» траекторий в точках разрыва правых частей системы совершается элементарно, если знак правой части второго из уравнений (2) не изменяется при переходе через линию сшивания. Так будет, если уо1 - г, т. е. если г «не слишком велико». Точки пересечения этой траектории с полосой ширины к будут X = -Y- г/ = Ti и а; = г/ = . Как

оказывается, величины ц я t, целесообразно рассматривать как параметры точечного преобразования.

Из уравнения (2), полагая S{x, г/)=1 для первого куска траектории и S{x, y)=l - r для второго и используя условия для концов кусков траекторий: х = - и, у = 0; х = - и + z, у = уо;

Z ~к

X = - У = Тр получим

г, = i+j + (1 - г) In \Z[Z + Уо - Л. Уо<Ц<1-г. (4)

Полагая далее S{x, у)=- - г для третьего куска траектории и S{x, г/)= - 1 -г для четвертого и используя условия для концов кусков траекторий

2 - к Z А- к с. г\

а: = -2-. У=Ц; Х=-, у = 1; X = V, У = 0,

получим

г\п{ + г)-г1п{ц + г) + ц--к = 0, (5)

v = -± + Z + {i + r)ln 0<S<°o. (6)

Уравнения (4)-(6) определяют требуемое точечное преобразование в нараметрической форме с двумя параметрами т) и ь-Разбиение фазового пространства {х, у) на тректории определяется взаиморасположением кривых (ti) и и = и{у\) на сов-меш;енных плоскостях (т), и) и (т), v). Исследование взаиморасположения кривых проводится элементарно при использовании ti и 5 как параметров.

Из (5) и (6) находим

Z( + r) dv t, „

и, следовательно, если существует точка пересечения кривых (ti) и г;=г;(т1), то она единственная и соответствует устойчивой, неподвижной точке преобразования.

Граничные значения кривых и = и{ц) и г; = г;(т)) будут u = {z + k)/2, v={z + k)/2

соответственно нри значениях параметров т) = г/о и т) = г/i (г/i определяется как корень уравнения (5) при ==0).

Для значений т), близких к 1 -г (т] = 1 - г - асимптота для и=и{ц)), будет u>v. Точка пересечения кривых и = и{г]) и 1; = г;(т1) будет поэтому существовать, если г/1 < г/о. Граница области существования неподвижной точки преобразования и соответствующего ей устойчивого предельного цикла определяется условием 1 = г/о.

Уравнение (3) совместно с уравнением

г1пг-г1п(г/о + г)+г/о-/(; = 0, (9)

полученным из (5) при = О и т) == г/о, рс 211

дает в параметрической форме уравнение поверхности (рис. 211), отделяющей в пространстве параметров область автоколебаний от области абсолютной устойчивости. Точкам ниже новерхности соответствует область автоколебаний. Точкам выше поверхности - устойчивость в большом (рпс. 212, а). Точкам по поверхности - вырожденный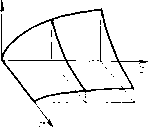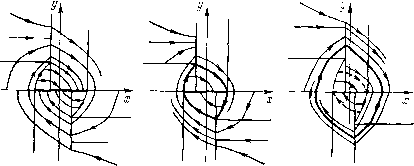

Рис. 212

двойной цикл, проходящий через концы отрезка покоя (рис. 212,6). На рис. 212, в изображены два склеенных предельных цикла - устойчивый и неустойчивый (неустойчивый обозначен штриховой линией).

Если г «велико» (уо> i - r), фазовые траектории подходят с обеих сторон к линиям сшивания у=-±уо и система (2) должна быть из физических соображений доопределена условием

• I г/о при x - {z - k)/2,

х-у, У-\ у при x{z-k)/2,

требующим, чтобы движение продолжалось по линии стыков траекторий (скользящий режим). Уравнение (4) теряет смысл. Любая траектория, сшитая из четырех кусков в верхней полуплоскости, начинающаяся в точке {-и, 0) и заканчивающаяся в точке (г;, 0), содержит кусок прямой г/= г/о, принадлежащий линии сшивания. В уравнении (5) параметр т] принимает фиксированное значение уо. Уравнения (5) и (6) будут в параметрическом виде (с параметром 5) связывать v ж к. Уравненпе (9) сохраняет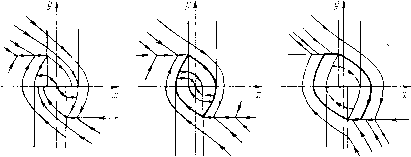

Рис. 213

смысл и для случая сколь угодно больших г. На рис. 213 изображены различные возможные типы разбиения фазовой плоскости для этого случая. В отличие от случая «малых г», здесь устойчивый предельный цикл будет вырожденным (на него переходят точки с континуума траекторий).

§ 3. Электрическая цепь с туннельным диодом. Рассматривается система [28]

i = г/-ф(a;), у =-а - %х~у, о>0, Я>0, (1)

где ф (х) - нелинейная функция, содержащая «падающий» участок. Система такого вида встречается при рассмотрении схем на туннельных диодах, а также в ряде других вопросов. Аппроксимируем (р{х) кусочно-линейной функцией, состоящей из трех линейных кусков. Наклоны к будем считать: падающего участка & = -ос2<0, восходящих A;=OCi>0. Фазовое пространство при такой аппроксимации разбивается на три части, в каждой из которых система линейна. В областях / и / лежат восходящие