
 |
|
Главная страница Приемы качественного исследования [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [ 29 ] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] б) характер узла {при т нечетном и Ат<0); причем при Ь<0 узел устойчивый, а при Ь > О - неустойчивый; в) состояние равновесия с одним узловым сектором и двумя седловыми {при т четном и любом знаке Am). При Ь < О узловой сектор устойчивый, при Ь> О - неустойчивый. Кроме того, если 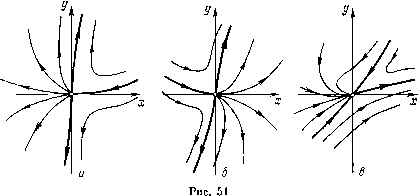 ЪАт < О, то траектории узлового сектора стремятся к О (при t -* +00 или при t -оо в зависимости ог знака Ъ) слева от оси у (рис. 51, а), а если ЬАт>0, то справа от оси у (рис. 51, б)). Состояние равновесия в слзгчае а) мы будем называть сложным седлом, в случае в) - седло-узлом, а в случае б)- сложным узлом ). Нетрудно видеть (см. §1), что, когда система имеет канонический вид (7), существует два направления, по которым траектории могут стремиться к рассматриваемому состоянию равновесия, это: О, я и я/2, Зя/2. На рис. 51, а, б представлен седло-узел в случае, когда система приведена к каноническому виду (7). Очевидно, в случае, когда в рассматриваемых координатах X ж у система не имеет канонического вида, направления, в которых траектории стремятся к началу координат, могут бьггь отличны от направления осей. Такой случай представлен для случая седло-узла на рис. 51, в. В дальнейшем особый интерес для нас будет представлять случай m = 2, который мы будем называть случаем простейшего двукратного седло-узла. В случае т> 2 будем называть состояние равновесия сложным седло-узлом. ) Хотя на рис. 51 оси координат нарисованы, но они не относятся к качественной структуре состояния равновесия и не надо придавать значения деталям взаимного расположения траектории и осей. ) Геометрически в рассматриваемом случае сложное седло и сложный узел ничем не отличаются от простого седла и узла. II. А (О, 0)=0, о (О, 0)=0. в этом случае, очевидно, оба характеристических корня состояния равновесия равны нулю. В рассматриваемом случае система линейным неособенным преобразованием приводится к виду dxIdt = y + Pt {х, у), dy/dt = (?* {X, у), где Р1(х,у) и 2(1) - аналитические функции, разложения которых по степеням х ж у начинаются с членов не менее чем второго порядка. Рассмотрим следующие функции: 1) функцию г/ = ф(а;), являющуюся решением уравнения у + Р*{х, г/)=0; 2) функцию у = -{х), определяемую формулой {x) = Q*{x, ф(х)); эта функция заведомо не равна нулю тождественно (в силу предположения об отсутствии общих множителей, отличных от постоянных у правых частей рассматриваемой системы), поэтому в разложении гз(а;) по степеням х заведомо будут отличные от нуля члены, и мы можем написать {x)=Q*{x, ф(а;))=а,а; + ...; а,0; 3) функцию о {х) = Pll, {х, ф {х)) + Qly {х, ф {х)) = 6„а;" + ... Функция о (ж), в отличие от {х), может тождественно обращаться в нуль. Рассмотрим сначала случай, когда а{х)ф{), так что при некотором п ЪпФО. Числа к, п ж коэффициенты йй и On характеризуют качественную структуру особой точки. При этом число к характеризует кратность общей точки изоклин (см. ч. II). Имеют место следующие теоремы. Теорема 3. Пусть к четное, к = 2т. Тогда: 1) в случае, если п<т, особая точка 0(0, 0) имеет качественный характер седло-узла (рис. 52); 2) в случае, когда п> т, суиествует одна полутраектория, стремящаяся к О при t -* -<», и одна полутраектория, стремящаяся к О при t +«>, все остальные траектории и при возрастании, и при убывании t выходят из окрестности О (г. е. окрестность особой точки О состоит из двух седловых секторов). Такое состояние равновесия мы будем называть вырожденным седло-узлом (рис. 53). Отметим, что рис. 53 выполнен при условии 6„ > О и ajm < О, а рис. 52 соответствует случаю Ь„ > О, аг™ < 0. Теорема 4. Пусть к = 2т -Ь 1 - нечетное число и am+i Ф О, и пусть V = Ь1 -f 4 (т -f 1) aam+i- Тогда: 1) если a2m+i > О, то особая точка 0(0, 0) имеет качественный характер седла (рис. 54); 2) если a2m+i < О, то особая точка имеет: а) характер фокуса или центра при п> т, а также при п = = m ц у < О [92]; б) характер узла, если п четное и при этом п<т или п = т и 10; в) одну замкнутую узловую {эллиптическую) область, две сопровождающие ее узловые области и одну седловую область 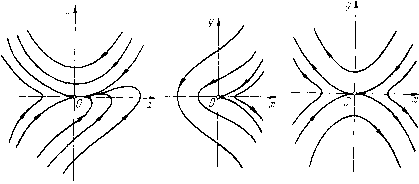 Рис. 52 Рис. 53 Рис. 54 (рис. 55), если п - нечетное число и при этом п < т или п = т и -iO. Рис. 54 и 55 выполнены при условии Ь„> 0; в случае 6„ < о расположение траекторий получается симметричным отображением относительно оси X. Нетрудно видеть, что в случае рассматриваемых состояний равновесия уравнение для определения направления, по которому траектории стремятся к состоянию равновесия: bk + {a-d)k-c = 0, (8) имеет двукратный нулевой корень (так как мы имеем a = d = c = 0, b ¥=0). Все стремящиеся к состоянию равновесия с Рис. 55 определенным направлением траектории стремятся к нему, касаясь оси X (см. рис. 52-55). Однако если состояние равновесия есть фокус или центр, то имеем, очевидно, случай, возможность которого была указана: когда, несмотря на наличие действительных корней уравненпя (8) и траекторий, стремящихся 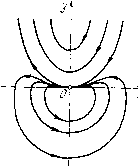 [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [ 29 ] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] 0.0141 |