которых существуют сложные состояния равновеспя меньшей кратности). Д.ля сложного состояния равновесия, для которого А = О, а ¥= О, все бифуркации исчерпывающим образом описываются числом и характером состояний равновесия, на которые это сложное состояние равновеспя может разделиться. Для сложных состояний равновеспя, для которых А = О, а = О, это не так. Действительно, как было указано, пз этих состояний равновесия возможно рождение предельных циклов. В настоящем параграфе мы рассмотрим двукратное состояние равновесия, для которого А = О, 0 = 0 н выполнены еще некоторые дополнительные условия. Такое состояние равновесия неоднократно встречается в рассматриваемых далее примерах, п знание его бифуркаций дает весьма полезную информацию при качественном исследовании конкретных систем.

Как мы уже указывали в гл. 4, состояние равновесия 0{ха, уа), для которого вьшолняются условия

Д(о, г/о) = а(хо, г/о) = 0,

I (0- Уа)\ + \ ру К Уо)\+\ qx (2-0- г/о) I + I Qy (-о- У о) I Ф 0. может быть приведено линейной заменой к виду

dxIdt = by + Р* {x, У) = Р {x, у), dy -dt = Q; {х, y) = Q {x, у). (1)

Пол агая

by + Р* {х. у) = v,

выражая из этого соотношения у через х и v ш переходя к переменным x ш V, мы придем к системе вида

dx/dt = v, dv/dt = QI {х, v).

Возвращаясь к прежним обозначениям для переменных и записывая полученную систему подробнее, мы получим

dx/dt = у, dy/dt = a2ox + anxy + ao2y + Q3{x, у), (2)

где Qsix, у) начинается с членов степени, большей или равной трем.

Нетрудно убедиться в том, что в силу предположения о дву-кратности состояния равновесия а2оФ0. В силу теоремы 3 § 2 гл. 4 это .состояние равновесия О имеет вид, представленный на рис. 105, а. Предположим, кроме того, что aii¥=0. Смысл этого условия будет ясен из дальнейшего.

Будем наряду с системой (2) рассматривать всевозможные, достаточно близкие к ней до ранга 3 системы. Так как качественный характер тех близких систем, у которых в окрестности 0(0, 0) нет ни одного состояния равновесия, очевиден (рис. 105,6), то мы обратимся к рассмотрению близких систем, имеющих состояния равновесия. Такие близкие системы можно,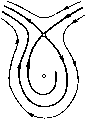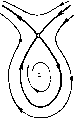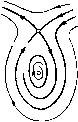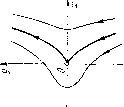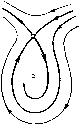

1 = [а2о«11 + (aib,e)l,

где /(а.й, е) -функция, зависящая от коэффициентов а,» в разложении 6*2(х, у), в которых 1 + к>Ъ. Так как в силу предположения аговиО, то для всех достаточно близких систем (3) a2oaiiTO п, следовательно,

L:¥=0.

Такнм образом, сложный фокус, возможный у близких систем (прп р, = 0), является устойчивым или неустойчивым в зависпмостп от знака выражения агоЯц, и из него может рождаться единственный цикл - соответственно устойчивый или неустойчивый (рис. 105, е). Однако того факта, что нз сложного фокуса системы (3) может рождаться единственный предельный цикл еще недостаточно для того, чтобы сделать заключение о том, что в достаточно малой окрестности состояния равновесия О системы (3) может быть только одпн предельный цикл, так как предельные циклы могут еще появляться из двукратных предельных циклов, появляющихся пз «уплотнения траекторий».

Если предполагать, что цикл единственный, то для различных достаточно близких к (2) систем (3) возможна, кроме указанных выше, одна из качественных структур, представленных на рис. 105, ж, 3.

Отметим, что знание возможных бифуркаций двукратной точки с двумя нулевыми корнями может оказаться весьма полезным при качественном исследовании конкретных динамических систем.

как нетрудно показать, всегда представить в виде

dx/dt = у, dy/dt = -ех +НУ+ Q2ix, у), Qzix, y) = a2oX + auxy + ao2y + Q3ix, у),

где 3(2:, у) начинается со степеней по х и у, не меньших трех. Нетрудно впдеть, что в некоторой достаточно малой окрестности состояния равновеспя 0(0, 0) системы (2) у всевозможных систем (3) может быть: 1) одно двукратное состояние равновесия того же типа, что и у исходной системы; 2) одно двукратное состояние равновеспя типа седло-узел (при 8 = 0, цФО) с устойчивым узловым сектором при ц < О, п неустойчивым при р, > О (рис. 105, в, г); 3) два грубых состояния равновесия: узел пли фокус и седло (узел при \i0, еФО п р, > Аг и фокус при цФО, е¥=0 и р,2<4е2); 4) два состояния равновесия - сложный фокус и седло при р. = О, е = О (рис. 105, д).

Непосредственным вычислением устанавливается, что первая ляпуновская величина сложного фокуса имеет вид