
 |
|
Главная страница Приемы качественного исследования [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [ 157 ] [158] [159] [160] [161] [162] [163] показано исчезновение двукратного состояния равновесия седло-узел, возникшего в результате слияния двух простых - седла и устойчивого узла. В двумерных системах два седла не могут слиться, образуя двукратное состояние равновесия, но такая возможность появляется в системах с числом измерений, большим двух. Возможные бифуркации простейшего сложного фокуса с отличной от нуля первой ляпуновской величиной: либо фокус становится грубым той же устойчивости, что и сложный фокус, либо из сложного фокуса рождается предельный цикл, а сложный фокус преврап];ается в седло-фокус (см. [37*]). Седлофокус 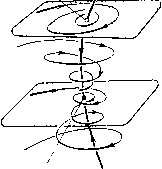 Устой.ча8о!й. <ро\ус Сложная особая точна селофонус-фокус 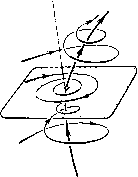 Рис. 253 Аналогичны бифуркации для сложного седло-фокуса: либо он делается грубым, либо из него рождается седловой предельный цикл, а седло-фокус становится грубым фокусом, устойчивым или неустойчивым (см. [37*]). Возможны бифуркации, полностью аналогичные бифуркациям седло-узла на плоскости. Если сепаратриса седло-узла или седло-фокуса-фокуса идет в него же и при t +оо, и при t )--оо, то при исчезновении состояния равновесия появляется единственный предельный цикл, устойчивый или неустойчивый в зависимости от того, был ли неустойчив или устойчив узел или соответственно фокус, от слияния с которым был получен седло-узел или седло-фокус-фокус. Если одна из сепаратрис седло-седла возвратцается в него же, то при исчезновении седло-седла появляется единственный седловой предельный цикл [137, 47*]. Рассмотрим бифуркации предельных циклов трехмерных динамических систем. Для таких предельных циклов Ляпуновым были введены величины, полностью аналогичные первому, неравному нулю коэффициенту в функции последования в окрестности замкнутой траектории на плоскости. Простейшими негрубыми предельными циклами являются циклы с первой ляпуновской величиной, не равной нулю. Таких предельных циклов в 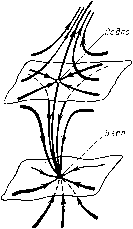 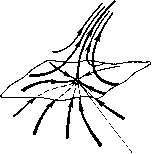 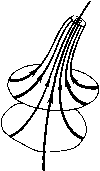 Сложная осодая точка Состояние равновесия исчезло Рис. 254 трехмерном пространстве три типа. Предельный цикл первого типа аналогичен двукратному предельному циклу на плоскости. При малых изменениях правых частей динамической системы он или разделяется на два грубых предельных цикла - устойчивый (соответственно неустойчивый) и седловой, или исчезает. Цикл heycvjutuobiu 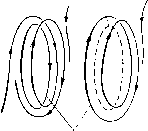 Устойчидьй цакп Рис. 255 второго типа может быть либо простым негрубым - устойчивым или неустойчивым, либо негрубым седловым. В первом случае от него при малых изменениях параметров либо отделяется двухоборотный с периодом, близким к удвоенному периоду од-нооборотного цикла (рис. 255), а одпооборотный цикл делается седловым, либо он становится грубым устойчивым. Соответственно во втором случае от него либо отделяется двухоборотный седловой цикл, а остающийся однооборотпый становится простым циклом, либо он делается грубым седловым. От цикла третьего типа - одпооборотного, усто11чивого - рождается устойчивый двумерный тор (рис. 256), а однооборотпый предельный цикл делается неустойчивым. Разбиение на траектории самого тора может быть очень сложным. Оно может включать незамкнутые траектории, устойчивые по Пуассону (незамкнутые самопредельные), или пары устойчивых и неустойчивых замкнутых траекторий, являющихся предельными для других траекторий па торе (см. [13*, дополнение]). В трехмерной системе аналогом сепаратрисы двумерной системы, идущей из седла в другое седло, является либо касание сепаратриспых поверхностей разных седел, либо «включение» сепаратрисы одного седла в сепаратриспую поверхность другого, либо совпадение изолированных сепаратрис двух седел; а- и ш-сепаратриспые поверхности седловых предельных циклов Устойчивый аикл Неустойчивый цинл могут касаться вдоль общей траектории, а также пересекаться. Общая траектория а-и м-сепаратрисных поверхностей седлового предельного цикла называется гомокли-нической траекторией. Структура окрестности гомоклини-ческой траектории чрезвычайно сложна и исследовалась многими авторами, начиная с Пуанкаре и Бирк-гофа. Наиболее полное рассмотрение в [138]. Аналогом сепаратрисы, образующей «петлю», является в трехмерной системе случай, когда изолированная сепаратриса седла включается в сепаратриспую поверхность того же седла. Целый ряд основных случаев бифуркации такой сепаратрисы, 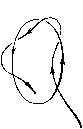 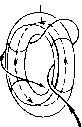 Рис. 256 [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [ 157 ] [158] [159] [160] [161] [162] [163] 0.0131 |