систем). На рис. 194, в-г - образование, аналогичное седлу, сшитое из обыкновенных траекторий с отрезком неподвижных точек (на концах этого отрезка нет состояний равновеспя). На рис. 195 отрезок неподвижных точек вместе с некоторой окрестностью аналогичен седло-узлу. На рис. 196, а - аналог двукратной точкп, для которой 0 = 0 (см. гл. 4); на рис. 196, б - аналог седло-узла.

Этпми примерами мы здесь ограничиваемся.

Если в рассматриваемых дальнейших конкретных примерах сшитых систем встретятся еш;е другие случаи доопределения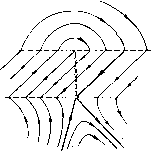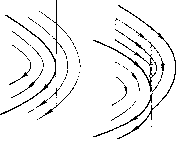

Рис. 195

Рис. 196

или другие возникающие при сшивании особенности, то мы обсудим их также прп рассмотрении соответствующей конкретной сшитой задачи.

§ 4. Бифуркации в сшитых системах. Метод Понтрягина для сшитых систем. Сшитые динамические системы, возникающие из приложений, всегда содержат параметры, и при изменении параметров качественная структура рассматриваемой системы может, очевидно, изменяться.

Мы рассмотрим простейшие возможные в сшитых системах бифуркации (изменения качественной структуры) при естественном предположении, что при всех рассматриваемых значенхшх параметров линии сшивания остаются неизменными.

Прп этом, очевидно, нам достаточно рассмотреть только би-фуркацхш сшитых особых траекторий, так как бифуркации траекторий, целиком лежащих в какой-либо из частных областей Gi - те же, что и описанные в гл. 10, 11.

Естественно выделить и рассмотреть следующие простейшие бифуркации, аналогичные простейшим бифуркациям аналитических динамических систем:

ai) бифуркации сшитого состояния равновесия типа фокус (см. рис. 188);

аг) бифуркации неподвижной точки типа фокус - квазифокуса (см. рис. 192, а);

6i) бифуракции СШИТЫХ предельных циклов;

Bi) бифуркации сшитых сепаратрис, идущих из седла в седло (седла могут быть как сшитыми, так и несшитыми);

Вг) бифуркации сепаратрис седлообразных точек покоя (сшитых илп несшитых), идущих из седлообразной точки покоя в такую же точку покоя или седло (сшитое или несшитое);

ri) бифуркации сшитого седло-узла;

Гг) бифуркации сшитых сепаратрис седло-узла (сшитого или несшитого), выходящих из седло-узла и возвращающихся в него же.

Кроме указанных бифуркаций, в сшитых системах могут быть также некоторые специфические для таких систем бифур-кацпп. В силу того, что в сшитых системах аналогами состояний равновесия могут быть дуги притяжения или отталкивания (см. рис. 193, а), состоящие из неподвижных точек, или область, заполненная замкнутыми траекториями, и т. п., то, естественно, встречаются также бифуркации таких образований, аналогичные рождению предельного цикла из фокуса. Однако мы не будел! их здесь рассматривать особо, а рассмотрим их, если они встретятся в конкретных примерах. Ниже мы приведем рассмотрение некоторых из перечисленных выше простейших бифуркаций.

1. Сложный сшитый фокус и рождение из него предельного цикла [22]. Пусть дана сшитая система

х = ах + Ьу + Р{х, у),

y = cx + dy + Q{x, у),

х = а*х+Ь*у + Р*{х, у),

L J L /1/ ч х>0. (II)

y = cx + dy + Q{x,y), >

Приведенная система имеет частный вид, ввиду того, что у обепх систем (I) и (II) второе уравнение одно и то же. Однако такого вида сшитые системы часто встречаются. Так, например, если рассматривается уравнение второго порядка

х + f{x, х) + G{x, х) = 0,

в котором f{x, х) и G{x, х) кусочно-непрерывны, то оно приводится к системе вида (l) -(II); одно из уравнений будет одним и тем же во всех областях сшивания. Отметим, что сшивание вдоль отрезка прямой х = О яе носит частного характера, т. е. к этому случаю мы всегда можем прийти, делая надлежащую замену переменных. Если уравнение дуги сшивания, являющейся аналитической дутой, есть

fix, У) = 0,

т)* = (0*1* + о*т)* + Q*{I*, т)*).

24 Н. Н. Баутин, Е. А. Леонтович

(Вг)

то нужно ввести новое переменное

f{x, у)=и.

Сшитая система, заданная с помощыо (I) -(И), имеет точку 0(0, 0) сшитым состоянием равновесия. Функции Р{х, у), Р*{х, у), Q{x, у)- степенные ряды, начинающиеся с квадратичных членов:

Р(х, у) = аох + аху + +

Р* {х, у) = alox" + atxy + ау" +

Q {х, у) = 202 -Ь Ъху + ЬоаУ -Ь • • •

Предположим, что для системы (I) (продолженной на линию сшивания х = 0) состояние равновесия 0(0, 0) является фокусом, т. е. корни соответствующего системе (I) характеристического уравнения

X - {a + d)k + ad- Ьс = О

- комплексные сопряженные:

А,1 = о + ш. Яг = о - ш. Линейным преобразованием

приводим систему (I) (рассматриваемую в некоторой окрестности начала) к каноническому виду:

Е = оЕ-шт1-ЬР(Е, т)),

- (Bl):

Предположим, что и для системы (И), продолженной за линию сшивания X = 0, начало О также является фокусом, т. е. соответствующее системе (II) характеристическое уравнение Х*2 (а* + d)X* + a*d -Ъ*с = 0

имеет комплексные сопряженные корни

Я* = о* -Ь ico*, Я* = о* - т*.

Линейным преобразованием

1* = х, г]* = -х-у (2)

приводим систему (II) к виду каноническому:

I* = 0*1* - Ш*Т)* + Р*(Е*, Т)*),