
 |
|
Главная страница Приемы качественного исследования [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [ 132 ] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] Предельных циклов нет. Фокус неустойчивый. Структура разбиения фазового пространства изображена на рис. 205, i. При 0 = 0 функция г)() тождественно обращается в нуль на интервале {-а, -Ь/2) и сохраняет положительное значение      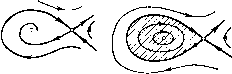 Рис. 205 на интервале (-Ь72,0). Существует континуум замкнутых кривых, окружающих состояние равновесия типа центр. Петля сепаратрисы не может существовать, так как г)(0)¥=0; оэ-сепарат-риса седла скручивается с границы области, заполненной замкнутыми кривыми; а-сепаратриса седла уходит в бесконечность по верхнему полуцилиндру (рис. 205, i-2). При о > О фокус становится устойчивым. Если о достаточно мало, то на интервале {-а?, -Ъ12) будет г)()<0, но сохранится г)(0)>0. На интервале (-Ь/2,0) будет существовать k = h\ - корень функции г)(fe), соответствующий неустойчивому (tfi(fei)>0) предельному циклу, возникшему из границы области, заполненной замкнутыми кривыми (рис. 205, 2). При возрастании а кривая tfi(fe) будет опускаться - при этом корень tfi(fe) будет возрастать - и для достаточно больших h функция if)(fe) становится отрицательной на всем интервале {-а, 0). Предельных циклов нет. Фокус устойчив. Структура разбиения фазового пространства однозначно определяется (рис. 205,4). Исчезновение корня h = h\ при переходе от структуры рис. 205,2 к структуре рис. 205, 4 может происходить либо при возрастании ho до нуля (этому соответствовало бы влипанпе и е-устойчивого предельного цикла в петлю сепаратрисы седла), либо ири слиянии его с другим корнем функции г)(/г). Не проводя подробного исследования поведения функции г)(/г) при разных а, можно ио знаку седловой величины заключить, что при возрастании а реализуется именно последний случай. Седловая величина, определяемая выражением (3), имеет при а>0 отрицательное значение и, следовательно, к петле сепаратрисы может стянуться или из нее появиться лишь устойчивый предельный цикл. Отсюда следует, что обращение в нуль величины г)(0), соответствующее возникновению петли сепаратрисы, должно предшествовать исчезновению корня h = h\. При перемене знака г)(0) (когда г)(0) становится отрицательным) появляется второй корень /г =/гг функции г)(/г), убывающий с возрастанием а и соответствующий устойчивому (г)(/гг)<0) предельному циклу. При дальнейшем возрастании а корни h\ и /гг сближаются, сливаются и исчезают. Описанному процессу соответствует на фазовой плоскости смена структур, представленных на рис. 205: рис. 205, 2-3 (г?(0) = = 0)-возникла петля сепаратрисы; рис. 205,5 (/г1</гг<0) - из петли сепаратрисы возник устойчивый предельный цикл; рис. 205,5-4 (/г1=/гг)-возник двойной полуустойчивый предельный цикл; рис. 205,4 (1;(/г) < 0)-циклов нет. Приведенные простые рассуждения дают строгое доказательство существования области пространства параметров, для точек которой система (1) имеет по крайней мере два предельных цикла. Непосредственное исследование функции г)(/г) позволяет убедиться, что г)(/г) не может иметь более двух корней. Это исследование, однако, довольно громоздко [67]. ГЛАВА 19 КАЧЕСТВЕННОЕ ИССЛЕДОВАНИЕ СШИТЫХ СИСТЕМ МЕТОДАМИ ТЕОРИИ БИФУРКАЦИИ § 1. Кусочно-линейная система с тремя параметрами. Рассмотрим дифференциальное уравнение [71] Полагая x + all-F{x)]x + F{x) = i. Р{х) = - х при F{x) = - х + 2 при и вводя новые переменные и параметры, приходим к системе вида dxjdt = у, dyldt = - а: - Ihy + а dxidt = г/, dyjdt = x - 2hy -Ь а - л д 3 (1) Будем рассматривать фазовую цилиндрическую поверхность склеенной системы, развернутую на часть плоскости, соответствующей неравенствам -л/2 а; <Зя/2 (рис. 206). Прямая х = л12 разбивает рассматриваемую часть плоскости на области 1 ш 2, в каждой из которых фазовые траектории определяются соответственно линейными системами. Прямые х = -я/2 VI х = Зя/2 отождествляются. Склеенная система имеет два состояния равновесия: Oi(a, 0) и 02(л -а, 0). Точка Oi - устойчивый фокус при 0</г<1, устойчивый узел при h>l. Точка Ог -всегда седло, сепаратрисы которого определяются уравнениями У-(-К±: Vhl+i) 1х-{л~ а)]. 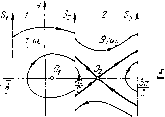 Рис. 206 [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [ 132 ] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] 0.0136 |