ТИПЫ ОСОБЫХ ТРАЕКТОРИЙ И ЯЧЕЕК

ИЛИ аналитического многообразия

F{x, у, Z, и, V, ...) = 0,

естественно ввести понятие грубости кривой или многообразия.

Рассматривая общие точки двух кривых

Fiix, у) = 0, F2ix, i/) = 0,

естественно ввести понятие грубости расположения двух кривых и т.д.*).

Можно было бы указать еще целый ряд математических объектов другого характера, ири рассмотрении которых введение понятий грубости, а также степеней негрубости было бы весьма плодотворным.

§ 9. Типы особых траекторий и ячеек в грубых системах.

Необходимые и достаточные условия грубости налагают определенные ограничения на возможные в грубых системах типы особых траекторий.

Особыми траекториями в грубых системах, очевидно, являются: грубые состояния равновесия (узлы, грубые фокусы, седла), предельные циклы (грубые) и сепаратрисы седел. Нри этом а (ю)-сепаратрисы при t-+o (f -оо) стремятся либо к узлу, либо к фокусу, либо к предельному циклу.

Как уже было сказано, знание расположения этих особых траекторий (схема динамической системы) полностью определяет качественную структуру разбиения на траектории. В рассматриваемом случае грубых систем нужно знать число и характер состояний равновесия, число предельных циклов, взаимное расположение состояний равновесия и предельных циклов и ход сепаратрис.

Особые траектории разделяют область G на подобласти - ячейки, заполненные неособыми траекториями.

Укажем возможные в грубых системах типы ячеек. Нри этом будем рассматривать лишь ячейки, в границы которых не входят граничные для замкнутой области G точки. Нетрудно показать, что могут иметь место следующие возможности.

Рис. 93

*) Требование аналитичности может быть ослаблено. Достаточно потребовать, чтобы функции F{x, у), F{x, у, z, ц, v), Fi{x, у), F2{x, у) и т. д. имели непрерывные производные до порядка m Г

1. Ячейка двусвязна, и граница ее состопт либо из двух предельных циклов (устойчивого и неустойчивого), либо из предельного цикла и одного лежаш;его внутри этого цикла состояния равновесия, являющегося узлом или фокусом.

2. Ячейка односвязна, и в границу ее входят:

а) одно седло, три сепаратрисы этого седла: две, стремящиеся к седлу при t ->- +0О (i-)-оо) и одна - при t -оо {t +°°),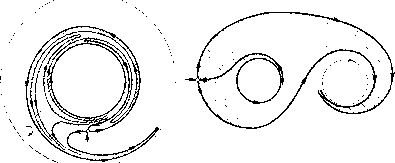

Рис. 94

и состояния равновесия или предельные циклы, являющиеся предельными для этих сепаратрис;

б) два седла, две сепаратрисы одного седла, стремящиеся к нему при t ->- -f-oo Hi-)-оо, п две сепаратрисы другого седла, стремящиеся к нему при t-+oo и t--оо, и два состояния равновесия (илн один или два предельных цикла) - устойчивое и неустойчивое, являющиеся предельными для этих сепаратрис.

Примеры ячеек типа а) и б) в случае, когда сепаратрисы стремятся к состояниям равновесия, представлены на рис. 93, а и 93, б. Когда предельными для сепаратрис являются предельные циклы, могут представиться различные случаи в зависимости от того, лежат сепаратрисы, входящие в границу ячейки, вне или внутри того предельного цикла, к которому они стремятся и в зависимости от того, совпадает ли положительное направление обхода предельного цикла с направлением обхода в сторону возрастания t или противоположно ему.

Рис. 95

На рис. 94 и 95 приведены некоторые ячейки типа а) и б) (полную классификацию см. [2, 3, 13]). Очевидно, число различных типов ячеек в грубых системах на плоскости конечно.

§ 10, Замечания по поводу определения грубой системы. Как

уже было сказано в § 1, определение грубой динамической системы BuepBbie было дано в предположении, что граница замкнутой области G, в которой рассматривается данная система и все близкие измененные системы, является циклом без контакта. Это предположение, очевидно, вызвано только тем, что формулировка определения грубости при нем упрощается.

Очевидно, однако, что при принятии такого определения мы не имели возможности говорить о грубости целого ряда систем, которые естественно считать грубыми. Так, например, пусть рассматривается динамическая система, которая имеет в некоторой области G (ограниченной замкнутой кривой) только одно седло или узел и седло. Такие системы мы должны, очевидно, считать грубыми. Но мы не можем пользоваться определением I, так как граница области G в этих примерах, очевидно, не может быть циклом без KoHTajtTa. Индекс замкнутой кривой, являющейся границей области G, в этих случаях, очевидно, не равен единице, и, следовательно, она не может быть циклом без контакта. Можно «подправить» определение I, делая более общие предположения относительно границы о бласти G. Например, можно допускать, что граница области G есть гладкая простая замкнутая кривая, имеющая конечное число касаний с траекториями системы (А) и не содержащая состояний равновесия (см. [155]). Однако всякие такие предположения относительно границы области всегда являются ограничениями, посторонними понятию грубости динамической системы. Ограничения на возможные границы должны вытекать из определения грубости. Кроме того, по смыслу понятия грубости из грубости системы в некоторой области G должна вытекать - непосредственно из определения - грубость системы в произвольной замкнутой области Go, содержащейся в G. Поэтому все указанные определения грубости (с условиями на границе) не полностью отражают смысл понятия грубости системы, а его отражает более сложное по форме определение Г. Отметим, что из определения Г непосредственно вытекает, что система (А)-j;py6aH в некоторой области G - груба во всякой области gG. Определение Г фактически используется также при рассмотрении негрубых систем, когда область, в которой рассматривается негрубая система, естественным образом разделяется на части, в которых система является грубой, и части, в которых система содержит негрубые элементы.

Кроме приведенных в настоящей главе определений грубости I и I в математической литературе существует еще несколько