цикла вто-

отображения в себя трансверсальной к циклу площадки о. Точка пересечения площадки с циклом есть инвариантная точка отображения.

Возможны следующие случаи грубых предельных циклов: устойчивый (неустойчивый) предельный цикл, когда все достаточно близкие к циклу траектории стремятся к нему при t -Ьоо (при t--оо), и седловой предельный цикл, который может быть двух типов. У седлового предельного цикла первого типа есть четыре двумерные сепаратрисные поверхности: две примыкающие к нему трубки и два примыкающих к нему кольца. На двух из сепаратрисных поверхностей (©-сепаратрисах) все траектории вида спиралей стремятся к циклу при t +00, на двух других (а-сепаратрисах) - при t -> рого типа сепаратрисными поверхностями являются два листа Мёбиуса (ю- и а-сепаратрисные поверхности). Все остальные траектории из окрестности седлового предельного цикла выходят из окрестности и при возрастании, и при убывании t. На рис. 252 представлеп седловой предельный цикл первого типа (сепаратрисные поверхности не показаны).

Подчеркнем одно характерное для многомерных систем свойство: сепаратрисные поверхности разных седел и седловых предельных циклов могут пересекаться или касаться по общей для них траектории. Случай их трансвер-

сального (без касания) пересечения является грубым.

Обратимся теперь к вопросу о перенесении понятий, введенных для двумерных систем, на трехмерные и больптего числа измерений и в первую очередь - понятия грубости. И здесь ситуация осложняется. Надо иметь в виду, что рассмотрение вопроса о грубости трехмерных систем тесно связано с рассмотрением грубости отображения плоской области в себя или плоскости в плоскость. Полностью необходимые и достаточные условия грубости трехмерных систем еще не установлены. Выделены только классы грубых систем, удовлетворяющих некоторым достаточным условиям грубости. Это, в первую очередь, системы Морса - Смейла, удовлетворяющие условиям:

1) число состояний равновесия конечно и все состояния равновесия грубые;

2) число замкнутых траекторий конечно и все траектории грубые;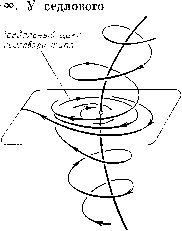

Рис. 252

3) сепаратрисные поверхности различных седел и седловых предельных циклов пересекаются трансверсально (без касания).

Несмотря на простую и естественную формулировку этих достаточных условий, возможная качественная структура систем Морса - Смейла может быть очень сложной. у таких систем может быть счетное множество «ячеек». Существуют также примеры грубых динамических систем со счетным множеством седловых предельных циклов с неограниченно увеличивающимся периодом. Впервые такой пример был построен американским математиком Смейлом (см. список дополнительной литературы [42*]). Примеры грубых систем со счетным множеством устойчивых или неустойчивых циклов с неограниченно увеличивающимся периодом отсутствуют. Доказательство того, что в грубых многомерных системах не может существовать счетного множества предельных циклов с ограниченными периодами, не представляет затрудненш!.

Понятие грубости динамической системы в многомерных системах не играет той роли, которую оно играет для двумерных динамических систем. Именно, метеорологом Лоренцем для целей предсказания погоды была выведена очень простая система трех дифференциальных уравнений

х = а{х~у), y=xz + rx-y, z = xy - bz {\.\

с постоянными параметрами о, г и 6 (см. [36*]). Оказалось, что при некоторых значениях параметров при отсутствии каких-либо устойчивых состояний равновесия или устойчивых предельных циклов у этой системы существует двумерное притягивающее множество «аттрактор»- множество чрезвычайно сложной структуры, к которому все траектории из некоторой его окрестности стремятся при t -> +оо,

В системе (1) есть седло, и это седло принадлежит аттрактору вместе со своими двумя изолированными сепаратрисами Fi и Гг. Аттрактору же принадлежит и счетное всюду плотное множество седловых предельных циклов с неограниченно увеличивающимся периодом и всюду плотное множество устойчивых по Пуассону траекторий. А главное, этот аттрактор негрубый: при сколь угодно малых изменениях параметра сепаратрисы Г] и Гг входящего в него седла меняют свое расположение - они то включаются в сепаратрисные поверхности одного из седловых циклов, входящих в аттрактор, то отделяются от нее. Так как седловые циклы всюду плотны в аттракторе, то при непрерывном изменении параметров аттрактор сохраняется, но его структура в силу описанного поведения сепаратрис Г] и Гг - непрерывно меняется. Таким образом, аттрактор Лоренца негрубый. Сложные режимы были обнаружены Лоренцем счетом на ЭВМ. Впо* следствии структура аттрактора Лоренца была рассмотрена в ряде работ, например в [25*]. Полное рассмотрение см. [9*, 10*].

) Возможность существования такого сложного негрубого притягивающего множества, как аттрактор Лоренца, вызвала огромный резонанс как в математике, так и в приложениях. Еще до появления уравнений Лоренца были известны «хаотические», «стохастические» колебания в системах, описываемых точными уравнениями без всякого присутствия вероятностных добавлений. Впервые такие движения были обнаружены в точно математически описанной модели часов, данной Н. Н. Баутиным ([12*, 35*]). Как оказалось, так называемый «пичковый режим» в лазере описывается теми же уравнениями Лоренца ([58*]).

В многомерных системах число типов простых и сложных состояний равновесия увеличивается с увеличением числа измерений.

Аттрактор Лоренца и его негрубость сохраняются и вообще при всех достаточно малых изменениях правых частей уравнения (1). А отсюда, очевидно, следует, что не существует сколь угодно близкой к системе (1) грубой системы и, следовательно, грубые системы не всюду плотны в пространстве трехмерных систем. Так как для двумерных систем всюду плотность грубых систем в пространстве динамических систем была чрезвычайно важным свойством, то в этом кардинальном вопросе разница между двумерными и многомерными динамическими системами очень существенна ). Тем не менее понятие грубости динамических систем трех и большего числа измерений - в простейшем случае систем Морса - Смейла или даже в еще более упрощенной ситуации, например, в случае систем Морса - Смейла с конечным числом ячеек, все же сохраняет свое значение. Большое значение (как математическое, так и для приложений) имеет также рассмотрение бифуркаций многомерных динамических систем через негрубые системы. Мы сделаем по этому поводу некоторые краткие замечания.

Естественно рассмотреть в первую очередь бифуркации простейших иегрубых элементов и, прежде всего, простейших негрубых состояний равновесия. В трехмерных системах, так же как и в двумерных, простейшими негрубыми являются состояния равновесия с двумя чисто мнимыми характеристическими корнями. Для них Ляпуновым аналогично двумерным системам введены «ляпуновские величины». В простейших из этих состояний равновесия первая ляпуновская величина отлична от нуля. В этом простейшем случае в трехмерных системах состояния равновесия могут быть двух типов: сложным фокусом (устойчивым или неустойчивым) и сложным седло-фокусом°). Далее, простейшими негрубыми состояниями равновесия в трехмерных системах могут быть двукратные состояния равновесия, возникшие в результате слияния двух простых. На рис. 253 показано образование двукратного состояния равновесия седло-фокус - фокус в результате слияния двух простых - седло-фокуса и устойчивого фокуса. При надлежащих изменениях правых частей системы двукратные состояния равновесия либо опять разделяются на простые, либо исчезают (см. [38*]). На рис. 254