4. Разбиение пространства параметров на области с различными качественными структурами фазового пространства. Проследим за сменой структур и бифуркациями при изменении р для фиксированного Я = Яо из интервала 1 < Я< pi. При р = О качественная картина разбиения фазового пространства эквивалентна представленной на рис. 169, 1. Бесконечность устойчива. Для р из интервала О < р. < Яо качественная картина будет эквивалентна представленной на рис. 169, 2. Бесконечность неустойчива. Из нее появился устойчивый предельный цикл. При р = Яо в точке (О, 1) появляется сшитое вырожденное состояние равновесия (если р, < р*) или сшитый седло-узел с устойчивой узловой областью (если ц, > р*). Качественная картина эквивалентна представленной на рис. 168, - / или 168, / соответственно. При дальнейшем возрастании \к сложная сшитая особая точка разделяется на две простые: седло 04(ф4, р4) и устойчивый фокус (узел) Оз(фз, рз). Качественная картина эквивалентна представленной на рис. 169,5. Обе со-сепаратрисы седла Oi идут в точку Ог (неустойчивый узел).

При р.л(Я-1)-Ь1 одна из СО-сепаратрис седла О4 уходит в бесконечность. Качественная картина эквивалентна представленной на рис. 169, 8. Между линиями Я = ц, и р = л(Я-1)-Ь1 при возрастании \к осуш;ествляются две

бифуркации сепаратрис: при не-

Pjjp 231 котором ц, = ц,"(Яо) возникает се-

паратриса, идугцая из седла О4 в седло Ol, и при ц, = ц,*(Яо) > р.*" (Яо) возникает петля сепаратрисы вокруг цилиндра.

Характер бифуркации при возникновении и разрушении петли сепаратрисы определяется знаком седловой величины

= {К + Qp)i = гйГ=1)"(" + - -

Кривая 04 = О касается прямой р, = л(Я - 1)+1 в точке Я = = р, = 1 и располагается справа от нее. Слева от прямой для бифуркационных значений параметров седловая величина имеет отрицательное значение. С возрастанием ц, при возникновении петли сепаратрисы к петле стягивается устойчивый предельный цикл.

При фиксированном Я = я1 из интервала p-i < Я < рг при возрастании ц на интервале я1 < ц, < л (я1 - 1)-Ь 1 осугцествляется лишь одна бифуркация: при \i = p (я1) возникает петля сепаратрисы вокруг цилиндра, к которой стягивается устойчивый предельный цикл. При фиксированном Я = Яг > Ц.2 при изменении ц,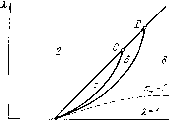

на интервале Яг < р < «» изменения качественных структур не происходит.

Кривые р = р"(Я) и р = р*(Я), соответствующие негрубым структурам, качественно эквивалентным изображенным на рис. 169, 5-6 и 169, 6-8, образуют бифуркационные кривые, начинающиеся в точке Я. = р = 1 и заканчивающиеся на прямой К= [1 соответственно в точках р = pi и р = рг.

На рис. 231 представлена без соблюдения масштабов схема разбиения пространства параметров \1>0, Х> I. Характер разбиения пространства параметров существенно отличается от разбиения для исходной системы (2) (см. рис. 167). В частности, здесь отсутствует область существования двух предельных циклов, охватывающих фазовый цилиндр. (Номера областей на рис. 231 соответствуют номерам качественных структур рис. 169.)

§ 2. Рассмотрение системы (2) прп аппроксимации, включающей отрезок параболы. Рассмотрим систему (2) при аппроксимациях

(- 2/л) ф -2, (2/л) ф, (-2/я)ф +2,

(2/л)ф -ь1,

1-(4/л) ф

(- 2/л)ф + 1,

sin ф ~ S3 =

COS ф •

- л/2], [-Л/2, л/2], [л/2, л];

[-л,0], [О, л/2], [л/2, л]

(см. верхний рис. 229 и рис. 232), отличающихся от (3) тем, что при аппроксимации cos<p отрезок прямой на интервале (О, я/2) заменен параболой. Такое изменение делает невозможным сложную бифуркацию с совпадением изоклин на отрезке и существенно меняет общую картину возможных бифуркаций.

Состояния равновесия на полосе -лфя будут Oi(-л/2, 0) - сшитое седло, 02(л/2, 0)-сшитый неустойчивый узел, Оз(фз, Рз) - узел или фокус, 04(ф4, Р4)- седло. Здесь ф4 - боль-шип корень, уравнения

Рис. 232

Ф +

(Я - ц)

= 0, 0<ф<л/2,

2ц 41

а фз - либо меньший его корень, если Я - р > О, либо определяется по формуле, приведенной в начале § 1, если Я - р, < 0. Величины р4 и рз находятся из уравнений соответствующих изоклин.

В пространстве параметров яа кривой - 4рЛ, -Ь 1 = О (р > 1/2) сливаются точки Оз и О4; на прямой Я = 1 - точки О4

И Оч. В плоскости параметров границей области существования только двух точек (Oi и Ог) будет отрезок прямой Я = 1, О < < ц < 1/2 и ветвь кривой \i - 4м.Я + 1 = О, \к> 1/2.

1. Рождение предельного цикла из фокуса. Фокус Оз меняет устойчивость на кривой

Оз (Р; + <?;)з = (1 - /l-4tiA + 4.u) - 2л = о,

начинающейся в точке (А = 1, ц = (2 + я)/(2 + 2.п)) и заканчивающейся на кривой 4ц, - 4ц,А +1 = 0, которой она касается в точке В:

ц = [ (4 + п)/4л] = (Хо, А = (2 + л) / [л (4 + л) ] "\

При переходе через кривую Оз = О в направлении возрастающих \1 фокус из неустойчивого становится устойчивым и из него появляется неустойчивый предельный цикл (первая ляпуновская величина для точек кривой Оз = О имеет значение

2. Структура разбиения фазового пространства на граничной кривой, разделяющей области двух и четырех точек. Точкам на кривой 4р- - 4Ац, + 1 = О (Ц>1/2) соответствует фазовое пространство с особой точкой седло-узел, возникшей от слияния точек Оз и Oi. При ц = ро совпадают направления, но которым траектории могут идти в особую точку, и седло-узел становится вырожденным. При переходе через значение р, = седло-узел с неустойчивой узловой областью (ц,<Хо) переходит в седло-узел с устойчивой узловой областью (ц,>ц,о). Для малых ц, сепаратриса седла Ol накручивается на предельный цикл, охватывающий цилиндр; со-сепаратриса седло-узла для больших ji имеет всюду отрицательный наклон и, следовательно, предельных циклов нет. При возрастании ц, вдоль кривой 4ц, - 4ц.А -Н + 1 = 0, ц, > 1/2, последовательность качественных картин, переходящих одна в другую, будет такая же, как на рис. 168.

3. Разбиение пространства параметров на области с различной качественной структурой фазового пространства. Обращение в нуль седловой величины

а, (р; + <?;)4= (1 + /i=w+v) - 2

происходит на кривой, касающейся граничной кривой в точке В и имеющей асимптоту Л = 1 +• 2/л. Седловая величина отрицательна выше кривой 04 = 0.

Отправляясь от известных структур разбиения фазового пространства на граничной кривой, можно проследить смену качественных структур нри возрастании \i, повторяя почти дословно