1) сложный фокус делается грубым той же устойчивости, что и сложный фокус;

2) сложный фокус делается грубым фокусом противоположной устойчивости, и при этом из него появляется («рождается») предельный цикл той же устойчивости, что и сложный фокус.

(См. рис. 117, 118, на которых представлены бифуркации сложного фокуса в случаях 1) и 2).)

Точнее: если О - устойчивый (неустойчивый) сложный фокус первого порядка системы (А), то:

а) существуют ео > О, бо > О такие, что у всякой системы (А), бо-близ-кой к (А), в бо-окрестности О может существовать либо один устойчивый (неустойчивый) сложный фокус первого порядка (и ни одной замкнутой траектории), либо неустойчивый (устойчивый) грубый фокус и устойчивый (неустойчивы!!) предельный цикл;

б) при всякол18 > о (е < 8о) люжно указать б > О (б < бо) такое, что у всякой системы (А), б-близкой к (А), у которой в ео-окрестности О существует фокус или предельный цикл, этот фокус или предельный цикл цели-ликом лежит в е-окрестности О.

III. Бифуркации двукратного (двойного) предельного цикла.

Двукратным предельным циклом Lq (см. § 4 гл. 9) называется такой цикл, что в функции последования s = ais + azs+ ..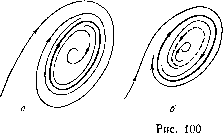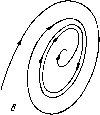

построенной на дуге без контакта lo, проведенной через какую-нибудь точку Lo, коэффициент ai = 1, а аг 0. Так как

= ехр J [Рх (ф, t;) + Qy (ф, т;)] df j,

то, очевидно, для двукратного цикла (рис. 100, а) т

[Pxi(P,) + Qy{4>,)]dt = 0, афО. о

При достаточно малых изменениях правых частей (удовлетворяющих условиям § 2 гл. 9), при которых система (А) грубая, возможны два случая:

1) двукратный предельный цикл разделяется на два грубых предельных цикла - устойчивый и неустойчивый (рис. 100,6);

2) двукратный предельный цикл исчезает (рис. 100, в).

IV. Бифуркации сепаратрисы, идущей из седла в седло. Воз» можны два случая.

IVa. Сепаратриса Lo идет из седла Oi в другое седло О» (см. рис. 91, а гл. 8).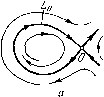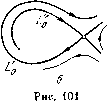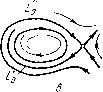

IV6. Сепаратриса Lq выходит из седла 0{хо, уо) и возвращается в то же седло (образует петлю) (рис. 101,а), и в седле 0{хо, Уо)

Ос = Ру {х, У о) + Qy {Хо, У о) Ф О-

Величину Ос мы назвали (см. гл. 9) седловой величиной. Если в седле О

ас< о,

то петля, образованная сепаратрисой Lq, устойчива (см. рис. 97). Если в седле О

ас>0,

то петля, образованная сепаратрисой Lq, неустойчива (см, рис. 96).

При всех достаточно малых добавках, удовлетворяющих условиям § 2 гл. 9, при которых система (А) является грубой, могут представиться следующие возможности.

Случай IVa. Сепаратриса Lo может разделиться на две сепаратрисы (Lq и Lo), и при этом могут быть два различных поведения этих сепаратрис (см. рис, 91, б, в).

Случай IV6. Сепаратриса Lo, образующая петлю в системе (А), разделяется на две Lq и Lq, причем:

1) При одном характере поведения сепаратрис L и L обе сепаратрисы Lq и Lq уходят из окрестности бывшей петли сепаратрисы Lo, так же как и все отличные от седла траектории, проходящие через близкие к Lq и Lq точки (рис. 101, б).

2) При другом характере поведения сепаратрис Lq и Lq от петли, образованной сепаратрисой Lo, появляется (рождается)

предельный цикл С, к которому стремится одна из сепаратрис L (или Lo) (рис. 101, б). При этом:

Если в седле 0{хо, у о) системы (А) седловая величина а с была отрицательна, т. е.

Ос = Рх {Хо, Уо) + Qy {Хо, Уо) < О

(т. е. петля, образованная в системе (А) сепаратрисой Lo, была устойчива), то рождающийся из петли предельный цикл устойчив (как на рис. 101).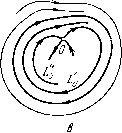

Если седловая величина Ос была положительна, т. е. Ос = рх {Хо, Уо) + Qy {Хо, Уо) > О

(т. е. петля была неустойчива), то рождающийся из петли предельный цикл неустойчив. То же справедливо в случае, представленном на рис. 102.

Точнее, можно сформулировать следующее предложение.

Если Lo - сепаратриса системы (А), идзчцая из седла Oi в седло Ог, то:

а) существуют 8о > О, бо > О такие, что у всякой системы (А), б-близкой к (А), в 8о-окрестности Lo седел Oi и Оа, существуют седла О и О и в 8о-окрестности Lo либо существует сепаратриса, идзчцая из седла в седло (и, кроме этой сепаратрисы и двух седел, больше нет ни одной негрубой особой траектории), либо нет сепаратрисы, идущей из седла в седло, и тогда система (А) является грубой;

б) npiлюбом 8 < 8о существует б <бо (б = 6(8)) такое, что у всякой системы (А), б-близкой к (А), у которой в 8-окрестности Lo с>тцествует сепаратриса, идущая из седла в седло, эта сепаратриса целиком лежит в 8о-окрестности Lo.

Если Lo - сепаратриса седла 0(хо, Уо) системы (А), образующая петлю, причем

Ос = Рх

(Vo) + 9i/(Vo)=0

а) существуют 8о > О, бо > О такие, что у всякой бо-близкой к (А) системы (А) в 8о-окрестности Lo лежат седло О и либо сепаратриса Lq седла О, образующая петлю (и, кроме Lq и седла О, нет ни одной особой