3 и 1. В ноднространстве параметров системы, имеющей особую точку типа центр, могут быть выделены области, вблизи которых существуют квадратичные системы с четырьмя предельными циклами как с вышеописанной, так и с другой топологической структурой, содержащей два седла и узел па экваторе. Сепаратрисы одного из седел идут к предельным циклам с распределением 3 ж 1 вокруг фокусов, сепаратриса другого седла идет к узлу на экваторе.

Рассмотрим систему

х = кх + кх + тху + пу, у =х + ах + Ъху.

Пусть Х = а = /7г = 0; тогда система (5) в Dq, определяемом условиями

к{п + Ъ)>а, п{п + Ъ)<0, п{Ь-к)<0,

(Do)

имеет топологическую структуру с двумя состояниями равновесия на плоскости (х, у) (типа центр) в точках (О, 0); (О, 1/ге) и одним седлом па экваторе сферы Пуанкаре (рис. 156А, а), сепаратрисой которого является интегральная прямая by + 1 = 0, от-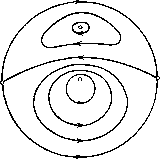

а lbjkjn)e.Bii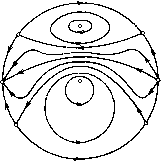

Рис. 156А

деляющая части полуплоскости (полусферы), заполненные замкнутыми кривыми.

В Dl, определяемом условиями

к{п + Ъ)>0, п{п+Ъ)<0, п{Ь-к)>0,

топологическая структура отличается от структуры в Do состояниями равновесия па экваторе.-В Di па экваторе два седла и узел (рис. 156А, б). Части полусферы, заполненные замкнутыми кривыми, отделяются в этом случае сепаратрисами, идущими из

седла в седло:

Ъ - к+п

п (6 - 2к)

2 (к+п)(Ъ-к+П)

кп (6 - 2кУ

Будем рассматривать систему (5) при условиях А: Х = 0, т(к + п)-а{2к-\-Ъ) = {), а¥=0, т¥=0

(в точке (О, 0) первая ляпуновская величина равна нулю).

Лемма 1. Существует множество GczDi, в каждой точке ко торого сепаратриса (6) является кривой без контакта для траекторий системы (5) при условиях А.

Доказательство. Производная от F{x, у) по t, взятая в силу уравнений (5) при условиях А, обращается в нуль на сепаратрисах (6) лишь в точках их пересечения с кривой

хЧ{Ь-2к) [{п{к + п)-{2к + Ъ){Ь-к)]у + {к + п){Ь-к + п)}

хЧ{у) = 0.

Гипербола (6) будет кривой без контакта, если прямая 1{у) = 0 ее не пересекает (на х = 0 контакт ложный). Это выполняется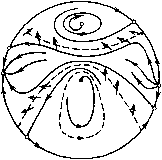

а Ъ-ЗК-5п>0 д b-ik-5n0

Off . т,

Л.=0,т=-]а,0<а<а1),Ъ<0,(Ъ,к,п)Е в Рис. 156Б

при условиях У1{0)<у<у2{0), где 1(у) = 0, а yi{0), 1/2(0)-координаты вершин гиперболы. Одно из этих неравенств всегда выполняется, другое сводится к

{2к + b){b-к) (&к + 2п + Акп- Ъ)-{к + п)Ч>0.

Множество G выделяется условиями (7) ж GD\ (рис. 1о6В).

Лемма 2. При условиях А существует положительная вели* чина ао(Ь, к, п) такая, что при (Ъ, к, n)<=G, \а\<ао система (5) имеет хотя бы один предельный цикл вокруг точки (о, 1/п), а при,

дополнительном условии п{Ь - Зк - 5п)> О - еще хотя бы один цикл вокруг точки (О, 0) при наличии в обоих случаях на экваторе сферы Пуанкаре двух седел и узла.

Доказательство вытекает из леммы 1 и теоремы Бенедиксона О существовании замкнутых траекторий, если учесть, что можно так выбирать а и. п, что в область, содержащую простой неустойчивый фокус в точке (О, траектории системы только входят, а из области, содержащей устойчивый фокус второго порядка в точке (О, 0) при (Ъ - Зк - 5п)п¥= О, только выходят (рис. 156Б,а)).

При Ь - Зк~5п0 цикл, существующий вокруг точки (О, 0), стягивается к фокусу и состояние равновесия меняет устойчивость (рис. 156Б, б)).

Поведение сепаратрис, попавших в области, ограниченные дугами и ветвями гиперболы (6), определяется однозначно. Предельные циклы, окружающие фокусы, являются для этих сепаратрис соответственно ю- и а-предельпыми множествами. Для сепаратрис, пе попавших в указанные области, существует несколько логических возможностей: они могут стремиться к узлу или седлу па экваторе, к фокусу или предельному циклу на плоскости. Однако при а<ао в силу близости к системе с особой точкой типа центр их предельным множеством может быть только узел па экваторе сферы Пуанкаре. При \а\<ао сохраняется топологическая структура, имеющая место при сколь угодно малых а.

Теорема 1. Если для системы (5) выполняются условия леммы 2, то существуют такие малые добавки к коэффициентам системы, разрушающие условия А, при которых измененная система имеет четыре предельных цикла при наличии на экваторе сферы Пуанкаре двух седел и узла.

Доказательство. Так как в точке (О, 0) при условиях А у системы (5) будет сложный фокус третьего порядка при 6 - ЗА; - 5ге = О, то можно найти такие малые добавки, разрушающие условия А, что в малой окрестности точки (О, 0) будет су-19*

b=const<0 Рис. 156В