чивый предельный цикл из бесконечности, который будет опускаться с возрастанием Я. Для значения Я = Я+ (ао; s) появляется двойной предельный цикл ниже устойчивого предельного цикла (двойной цикл не может возникнуть выше устойчивого предельного цикла, появившегося пз бесконечности, так как выше цикла при повороте поля по часовой стрелке с возрастанием % шаг спирали, накручивающейся на устойчивый цикл сверху, может только увеличиваться). С дальнейшим возрастанием X двойной предельный цикл разделяется на нижний устойчивый и верхний неустойчивый и осуществляется структура разбиения рис. 175,3. При дальнейшем возрастании "к устойчивый цикл опускается, неустойчивый поднимается. Так как для Я, > х* циклов уже нет, то в интервале Я" < Я, < х* необходимо осуществляются еще две бифуркации: слияние устойчивого и неустойчивого предельных циклов на бифуркационной кривой Я, = = Я+"(ао; s) и возникновение на бифуркационной кривой Я = Яо(ао; % s) петли сепаратрисы при стягивании к ней с возрастанием к устойчивого (так как седловая величина отрицательна) предельного цикла.

Проследим расположение бифуркационных кривых в плоскости (а, к). Бифуркационная кривая Я = Я+(ао; s) существует для всех значений а > ai и для значений а < аь достаточно близких к аь Кривая Я = Я,+(а; s) имеет отрицательный наклон. Последнее следует пз того, что на кривой с положительным наклоном при одновременном возрастании или убывании параметров а и Я векторное поле поворачивается монотонно и при этом двойной предельный цикл не мог бы существовать. Бифуркационная кривая Я = Я+(а; s) начинается в точке Я = О, а = аь существует в некоторой окрестности этой точки слева и по тем же причинам, что и кривая имеет

отрицательный наклон.

Кривая P(f + Qy = О не имеет в фазовом пространстве действительных ветвей, если а < Ask. Поэтому при условии а < <Ask не может быть более одного цикла, охватывающего фазовый цилиндр (гл. 6). Это обстоятельство помогает проследить поведение кривых Л,*" и Я,*"*.

Кривые к и при убывании а не могут идти ни в бесконечность (так как не могут пересекать прямую Я = х*), ни к оси к (так как не могут пересекать прямую а = Ask), ни к оси а (так как имеют отрицательный наклон). Кривые к* и к** могут при убывании а прекратиться лишь в угловой точке, соответствующей смыканию бифуркационных кривых Я+ и Для значений параметров, соответствующих этой угловой точке, система будет иметь тройной предельный цикл.

Бифуркационная кривая Я = Яо(а; s) существует на интервале О а аг. Любая прямая а = ао (О ао < аг) или к = = ki (OXix*) пересекает ее только один раз, так как поле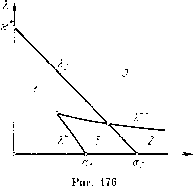

направлении при возрастании а или К поворачивается монотонно. Она проходит через точку а = О, К = к* (но определению X*) и точку а = аг, К = 0 (по определению аг (см. § 6)). Кривая Ко по тем же причинам, что и кривые Я* и Я*"*", имеет отрицательный наклон.

Замечание. Структуры на прямой К = 0 известны, лишь С точностью до дополнительного четного числа циклов, охваты-ваюш,их цилиндр (см. гл. 14), поэтому остается неустраненной логическая возможность суш,ествования «двойников» бифуркационных кривых Я* и

Выясним расположение кривой Ко относительно кривых Я* и Я""""*" в предположении отсутствия «двойников». Еслп нри возрастании К петля сепаратрисы вокруг цилиндра возникает и затем разрушается прежде, чем появляется двойной предельный цикл, то возникает разбиение фазового пространства на траектории без предельных циклов; со-сепаратриса седла, выходяхцая на верхний полуцилиндр, накручивается на цилиндр, уходя в бесконечность. При дальнейшем возрастании К предельные циклы возникнуть уже не могут, так как с возрастанием К ноле поворачивается по часовой стрелке и шаг спиралей на верхнем полуцилиндре при этом только увеличивается. Никакая часть кривой Ко не может располагаться ниже кривой К*. Поэтому кривые Ко и К не могут пересекаться.

Кривая Ко не может проходить и через угловую точку смыкания кривых К* и Я"""""". Такой точке должна соответствовать структура разбиения фазового пространства с тройным устойчивым предельным циклом и простой устойчивой петлей сепаратрисы на верхнем полуцилиндре (седловая величина не равна нулю и отрицательна). Наличие этих элементов в структуре разбиения фазового пространства возможно лишь при сухцествова-НПТ1 разделяющего их неустойчивого предельного цикла. Предположение о возможности такой структуры в угловой точке приводит к противоречию с предположением, что эта точка угловая а (поворот поля прп убывании а может перевести такую структуру в структуру с одним предельным циклом, осуществляющуюся слева от прямой а = 4sK, лишь с переходом через бифуркационную кривую а это невозможно, если начальная точка угловая).

Кривая Ко пересекает К справа от угловой точки. Разбиение пространства а, К для р = const (0<р<1) и s = const

представлено на рис. 176. Цифрами 0-3 отмечены области в пространстве параметров, соответствующие грубым структурам на рпс. 175, отмеченным теми же цифрами. Цифры указывают на число циклов. Негрубым структурам на рис. 177, помеченным двумя или четырьмя цифрами, соответствуют бифуркационные кривые на рис. 176,, разделяющие соответствующпе области. Значки * и на рис. 177 соответственно указывают на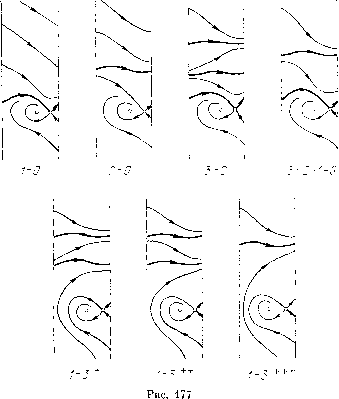

принадлежность к бифуркационным кривым Я""" и К. Преде.ть-ный цикл на рис. 177, i-5+, • трехкратный.

§ 8. Синхронный генератор с асинхронной характеристикой.

Рассматривается спстема [40]

d((>ldt = y, dyldt = i - sin (р-К {i - d cos (р) у. (1)

Будем предполагать {>0 ж 1>0 (другие возможные случаи сводятся к рассматриваемому заменой переменных).