рис. 215. На рис. 217 теми же цифрами, что и на рис. 216, отмечены грубые качественные структуры, соответствующие различным областям фазового пространства. Негрубым структурам на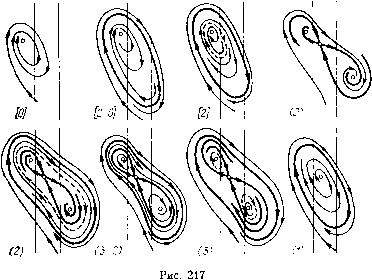

рис. 217, помеченным двумя цифрами, соответствуют бифуркационные кривые рис. 216, разделяющие соответствующие области (и соответствующие двойным циклам).

§ 4. Система со скачками на линии сшивания. Рассмотрим уравнение [126-128]

q> + 2h[l-bF{(f)](f+F{(f) = Q, F {ц, + 2л) = F {(f), (1)

в предположении, что характеристика (ф) имеет разрывы типа конечного скачка.

Пусть ффо -одна из точек разрыва. Эквивалентная уравнению (1) система

Ф = у, y=.Q-F{(f)-2h[l-bF((f)]y

не определена на прямой ф = фо. Поэтому движение изображающей точки системы при попадании ее на эту прямую нуждается в доопределении. Естественно получить его следующим образом. В интервале (фо -р., фо + р,) заменим характеристику F(<p) прямой, соединяющей точки [фо - р, (фо - 0) ] и [фо -Ь р., 7 (фо + 0) ]. Тогда на фазовой плоскости в полосе фо -р.<Ф<фо + М вместо

системы (2) будем иметь систему

./: - 2ау -

а; = ф-фо, p=.F(фo-0)-Q, f = F(фo + 0)-Q,

» = .(i + .ti).

На одной из прямых а; = d= р зафиксируем какую-нибудь точку с ординатой г/о- Может оказаться, что полутраектория х = = x{t, р), y = y{t, р) системы (3), начинаюш;аяся при t = 0 в. этой точке и проходяш;ая внутри полосы, при всех достаточно малых р вновь выходит из полосы при некотором f = i(p) в некоторой точке с координатами x = \i, г/==г/(р) (или а; = - р, У = 2/(1))• В этом случае примем такое доопределение: изобра-жаюш;ая точка системы (2), попав в точку (ф = фо, у = Уо), находится на прямой ф = фо в течение времени t, равного пределу f (р) при р О, после чего продолжает движение при ф >фо (илп Ф<фо) в соответствии с системой (2) при начальных условиях ф = фо, !/ = lini!/(p) при р 0. Если же рассматриваемая полутраектория системы (3) при всех достаточно малых р целиком лежит в полосе, то примем такое доопределение: изображающая точка системы (2), попав в точку (ф = Фо, У = Уо), остается на прямой неограниченно долго. Ситуации, которые представятся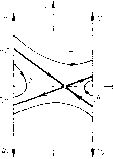

Рис. 218

при вычислениях, исчерпываются двумя указанными. Уравнение движения изображающей точки по прямой ф = фо в обоих случаях получим предельным переходом в уравнениях рассматриваемой полутраекторпи системы (3): у = Y{t) = limy(t, р) при р 0.

Перейдем к вычислениям. Выделим на прямой а; = - р полупрямые (рис. 218)

и{х = -[I, у = и>0}, Ui{x=-n, y = - ui<0}

И на прямой х = \1 полупрямые

V{x = p., г/ = г;>0), Viix = y = -Vi<0}.

Траектории системы (3) осуществляют точечные преобразования полупрямой и в полупрямые V и U\. Назовем их соответственно преобразованием Т и преобразованием S. Параметрические уравнения функции соответствия будут для преобразования Т

2(0 [г 2щц

Р [ cth ют -Ь

ехр {ат} sh мт

для преобразования S 2мр,р i-V

2щрр,

r-4=-v(cthcoT-il sh (ВТ 1 со у

и, =

с1Ьюе+ -ЩШ

со sh соО

со sh соО

Здесь т и 9 - параметры (время перехода изображающей точки системы (3) с полупрямой U соответственно на полупрямую V или Ul).

Рассмотрим случаи.

I. Y < О < Р, г = 2bh > 0. Состояние равновесия (3) есть седло, расположенное внутри полосы -р,<х<\1. Соответствующая картина фазовых траекторий приведена на рис. 218, а.

Пусть Цо - отрезок, отсекаемый на полупрямой U сепаратрисой, имеющий отрицательный наклон. Величина uo при р, -*

0. Поэтому, какую бы точку и на интервале и > ни фиксировать, при достаточно малых ]х она участвует в преобразовании Т. При этом первое из равенств (4) неявно определяет функцию т = т(l)- время перехода из фиксированного и на полупрямую У. Ее предельное значение при рО (приложеиие 1) есть

г In [гу/(гр-м)],

rp<u<r(P-Y), цг(Р-у).

Во втором из равенств (4) положим т = т(l) и найдем lim г; [т(l), i] при ц ~*" О- Это предельное значение (приложение И) есть

О, rP<u<r(p-Y),

U-r(p-Y), u>r(p-Y).

Фиксируем теперь какую-нибудь точку на интервале и < г. При малых р она участвует в преобразовании S. При этом пер-