Обозначим через Si, S2 и S3 полупрямые х --л/2, х~п/2 ш х = Зя/2, соответствуюп1;ие значениям г/ > 0.

Фазовые траектории системы осуидествляют точечные преобразования полупрямой Sl в 2 (преобразование Li) и полупрямой 2 в S3 (преобразование L2). Пусть Si, S2 и 5з - ординаты точек соответствуюп,их полупрямых; х/ац, В/шг - времена пробега изображаюп,ей точки (см. рис. 206) через области 1, 2, соответствующие преобразованиям Li и L2.

Величины Sl, S2, т, 0 принимают положительные или нулевые значения. Интегрируя линейные уравнения (1) в областях 1 и 2, обьганым образом получаем параметрические уравнения для функций соответствия.

Для области 1 получаем

5i(t, h,, а) =

3 (т, hj, а) = Sj (т, - h,, - а).

(Ll)

Здесь = Vl-hi, ki = hi/(oi и 0<h<i. Выражения для производных могут бьггь представлены в виде

sm t 3kjX

В случае h>i выражения для Si{r, hi, a) и 5г(т, hi, a) и производных получим, если в правых частях полученных выражений заменим sin т и ctg т соответственно через sh т и cth т.

Параметр т меняется в пределах от т = 0 (>S2(0) = 5i(0) = <») до значения т = т*, при котором Si или 2 обращаются в нуль. Тот или иной случай при О < /г < 1 реализуется в зависимости от знака выражения

(я/2 - а) Л" - (я/2 + а).

При h> i всегда реализуется случай 52(т*) = 0, 5i(t*)>0. Кривая Si=Si{S2) имеет асимптоту Si=S2 + 2nhi. Некоторые возможные виды кривой, соответствующие преобразованию Li, изображены на рис. 207.

Рис. 207, а соответствует случаю (я/2 - а) е i" - (я/2 + а) < О й, в частности, всегда реализуется при малых hi. Промежуточный между изображенными случай, когда кривая проходит через начало координат, соответствует т* == я и обращению в нуль выражения (2).

Для области 2 получаем

- а

©2cth9 - h),

Здесь (02 = 2 +1, k2 = /гг/оэг-

Выражения для производных могут быть представлены в виде

she -320

Параметр 9 меняется в пределах от 9 = О (52(0) = 53(0) = <») до значения 9 = °°. При этом оба предельных значения отличны от нуля:

5з(оо) = (я/2 + а) (Ы2 -h2)>0, S2M = (я/2 - а) (©2 + йг)> 0. Кривая = 53(52) имеет асимптоту 5з = 52 - 2я/г2.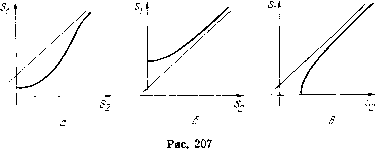

Вид кривой для h2<0 (только этот случай и будет рассматриваться) представлеп па рис. 208. Конечная точка кривой 5з: Л [(©2 +/гг) (я/2 - а), (шг - fe) (я/2-Ь а)] для малых /гг(-/г2< < а [(я/2-Ь а) (я/2 - а)] ") леясит выше асимптоты.

Для разыскания предельных циклов, охватывающих фазовый цилиндр, нужно рассмотреть преобразование L == /1L2, отображающее полупрямую 5] в 5з (5з отождествляется с Si) по траекториям системы. Неподвижным точкам этого преобразования соответствуют предельные циклы, охватьшающие цилиндр и расположенные в верхней части фазового цилиндра у>0. Для отыскания этих неподвижных точек надо найти точки пересечения кривых 5i = 5i(52) и 5з = 5з(5г), рассматривая кривые на совмещенных плоскостях (52, 5i) и (5г, 5з) (рис.209).

Нетрудно видеть, что бифуркации, при которых появляются или исчезают точки пересечения кривых = S\{S2) я 83=° = 8з{82), имеют место:

а) если точка А кривой 8з = 8з{32) лежит на кривой 5] = = 5,(52);

б) если асимптоты рассматриваемых кривых совпадают;

в) если рассматриваемые кривые касаются.

По аналитическим выражениям для кривых 5i (г) и 33(82) легко прослеживается только вторая из перечисленных бифуркаций (совпадение асимптот). Для бифуркаций а) и в) аналитические условия их осуш;ествления приводят к громоздким со-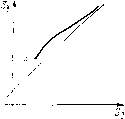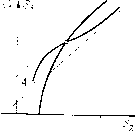

Рис. 208

Рис. 209

отношениям (особенно условия соприкосновения кривых). Дополнительное привлечение качественных методов позволяет су-ш;ественно упростить прослеживание бифуркаций. Покажем, что могут существовать два цикла, охватывающих цилиндр.

Так как для положительных ki и Аг (для положительных hi и А2) во всех точках пересечения кривых 81(82) и 83(82) выполняется неравенство

3) g2ftjT.f2.

ТО в этом случае может быть не более одной точки пересечения и эта точка соответствует устойчивому предельному циклу. Два предельных цикла не могут существовать при hi и А2 одинаковых знаков.

Проследим за последовательностью бифуркаций при некотором фиксированном А2<0 с возрастанием hi. Пусть асимптоты совпадают, т. е. hi +2 = 0.

Так как для больших 2 будет d.8i/dSl<:0, dS/dSlO и при расхождении асимптот с возрастанием hi асимптота для кривой 81(82) поднимается и располагается выше асимптоты для кривой 83(82), то при этом возникает точка пересечения кривых 81(82) и 53(52) (рис. 209), соответствующая устойчивому пре-