Р тР -Оф

Состояниями равновесия этой системы являются 01{-я/2, 0), 02{я/2, 0) и Оз(0, 1).

Нетрудно убедиться в том, что состояния равновесия Oi и О2 - седла, а также, что для состояния равновесия Оз(0, 1) характеристическое уравнение имеет чисто мнимые корни, и система в окрестности этого состояния равновесия имеет аналитический интеграл, т. е. состояние равновесия - центр.

Нетрудно, кроме того, непосредственно проверпть, что кривая

р = 3 cos ф

интегральная и является сепаратрисой, идущей из седла в седло. Наметив направления на траекториях, составляющих интегральную кривую р = О, мы получаем картину траекторий, изображенную на рис. 137, а

б) 1 > Я, > 0. Нри Я, < 1 у системы (2) три состояния равновесия:

0,(-я/2, 0), 02(я/2, 0) и Оз{фз, Рз),

где

Фз = arcsin Я,, рз = У1 - К.

в) Нри Я, > 1 у системы два состояния равновесия Oi и О2. Записывая для всех состояний равновесия соответствующее характеристическое уравнение

х2 - ох + А = О,

находим: 1) характеристические корни для состояния равновесия Оь

Х1 = -1, Х2 = 2(Я+1),

т. е. состояние равновесия Oi - седло при всех Я, > 0; 2) характеристические корни для состояния равновесия О2:

xi = 1, Х2 = 2{Я-1),

т. е. О2- седло при Я,< 1 и неустойчивый узел при Я,> 1.

) Здесь и далее для большей наглядности масштабы на рисунках не всегда соблюдены.

И, ВЗЯВ в качестве интегрирующего множителя М = 1/(2Ур), получаем интеграл системы

При 1 = 1 будет Х2 = о, т. е. значение Х = 1 является бифуркационным. Состояние равновесия Оз(фз, рз), существующее при Я, < 1, является неустойчивым фокусом или узлом.

При Я = 1 состояние равновесия Оз сливается с О2, образуя сложную особую точку, которая ири Я > 1 делается грубым неустойчивым узлом.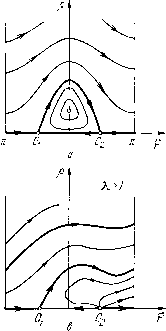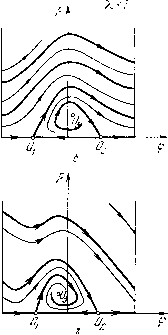

Рис. 137

Разность наклонов траекторий системы (2) при Я > О и Я = О есть

2р {x - sin ф) 2р sin ф 2рХ р - cos ф р - cos ф р - cos ф

При р - cos ф > О это выражение положительно, и, следовательно, выше сепаратрисы, и на сепаратрисе консервативной системы р = 3 cos ф, идущей из седла в седло, поле поворачивается на положительный угол. Поэтому нет циклов, охватывающих цилиндр. Так как

2Ур ф

ЗцУр

то у системы нет предельных циклов, охватывающих состояния равновесия (критерий Дюлака).

Сравнивая эту систему с системой (3), мы, так же как и в предыдущем примере, заключаем, что у системы (4) нет предельных циклов, охватывающих цилиндр.

Расположение траекторий представлено на рис. 137, г.

Пример 3.

d(fldt = y=P{(f, у), dyldt = Y -зшф- 2% = (?(ф, у).

(К рассмотрению этой системы сводится целый ряд задач: движение маятника с постоянным моментом, динамика синхронного мотора в простейшей идеализации, стабилизация скорости вращения двигателя постоянного тока часовым регулятором и др. В дальнейшем она будет использована и как система сравнения.) Эта система подробно рассмотрена в [162, 2, 3, 149, 39].

Приведем здесь исследование этой системы в простейших случаях:

а) = 0, = 0; система имеет вид

difjdt = у, dyldt = -sin ф. Очевидно, она имеет интеграл

Н (ф, У) = у- cos ф = С.

Картина траекторий представлена на рис. 138, а.

то нет и циклов, охватывающих состояния равновесия (критерий Дюлака). Расположение траекторий представлено на рис. 137,6 и 137, в.

Пример 2 [150].

d(f/dt = p - cos ((1=Р, dpldt = 2p{-np - sin(f) = Q. (4)

(Эта система получается пз системы (1) прн Х = 0.) При р = 0 мы получаем систему (соответствующую Я, = О предыдущего примера), изображенную на рис. 137, а.

При р > О у системы три состояния равновесия. В точках 6»1(-л/2, 0), 02(л/2, 0) будут седла.

Если положить

р = tg р, о < р < л/2,

то третье состояние равновесия будет

Оз(-р, cosp).

Оно является устойчивым фокусом или узлом. Так как