3) может совпадать с траекторией (полутраекторией, дутой траектории) системы (А).

Такой участок траектории называют отрезком скользящего движения.

§ 2. Возможные типы полутраекторий сшитых систем. При

дальнейшем описании свойств сшитых систем рассмотрим в первую очередь, так же как и в случае систем с аналитическими правыми частями, каков возможный характер отдельной траектории или полутраектории такой системы.

Пусть Мо{хо, г/о)-точка, принадлежащая области Gi я Lf - положительная полутраектория системы (А(), проходящая при t = to через эту точку. Рассмотрим возможное поведение при t > to. Возможны следующие случаи.

1) При всех t> to полутраектория Lf остается в области Gt, которой принадлежит конец Lf - точка Mq. Тогда Lf определена для всех t> to, и ее возможный характер такой же, как и у аналитической динамической системы. (В частности, если полутраектория Ll стремится к состоянию равновесия, то это состояние равновесия может лежать как внутри G,-, так и на границе Gi (на линии сшивания).)

2) При t, стремящемся к некоторому конечному значению t\ > to, иолутраектория Lf приходит в некоторую точку М на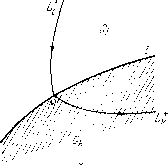

Рис. 185

линии сшивания I, являющуюся граничной для еще одной частичной области Gh {кФ1).

Рассмотрим случай, когда полутраектория L не касается линии I в точке М. Могут представиться следующие возможности:

а) траектория L системы (А), проходящая через точку М, не касается дуги I, и при возрастании t уходит от граничной дуги I внутрь области G. Тогда могут быть следующие случаи:

ai) положительная полутраектория системы (А) (с концом в точке М) считается непосредственным продолжением траекторпи Lf (так что в этом случае Lt непрерывно продолжается через линию сшивания) (рис. 185, а);

аг) полутраектория Lf кончается в точке М, так что точка М аналогична полуустойчивому состоянию равновесия (рис. 185, б);

б) траектория системы (А) «втыкается» при возрастании t в точку М. Тогда:

6i) точка М считается аналогичной состоянию равновесия (рис. 186, а);

Рис. 186

бг) точка М считается точкой траектории, совпадающей с граничной кривой I (рис. 186, б);

в) из точки М изображающая точка, двигавшаяся по Lf, перескакивает в некоторую другую точку N дуги I, а траектория Lt системы (Aft), которая из точки N при возрастании t входит

в область Gft, считается продолжением Lt. Возможно также, что часть дуги I между точками М ш N является продолжением Lf, а дальнейшим продолжением Lt является полутраектория L системы (Aft), выходящая из точки N (рис. 187).

Мы не будем здесь рассматривать случай, когда траектория касается в точке М дуги I (в этом случае иногда возможны те же условия продолжения или остановки, что и рассмотренные выше), а также не будем обсуждать другие возможные случаи доопределения на линии сшивания и будем обращаться к ним, если они будут встречаться в рассматриваемых далее конкретных задачах.

Отметим некоторую существенную особенность, указанную доопределениями траекторий в сшитых системах, соответствую-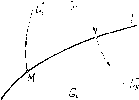

Рис. 187

щих реальным задачам: полутраектория доопределяется всегда однозначно при возрастании t. Однако в сторону убывания t траектория, вообще говоря, не определяется (и однозначность доопределения при убывании теряется).

§ 3. Особые траектории сшитых систем. Рассмотрим теперь вопрос об особых траекториях сшитых динамических систем. Очевидно, все особые траектории каждой из частичных систем (Ai), целиком лежащие в этих областях (состояние равновесия, предельные циклы сепаратрисы состояний равновесия, лежащие в Gi), являются особыми траекториями сшитой динамической системы. Кроме того, рассмотрим другие особые траектории склеенной системы.

а) Состояния равновесия О какой-либо из систем (Ai), определенной в области G„ лежащие на линии склейки Z, граничной для Gi. При этом здесь возможны следующие два случая:

ai) точка О является состоянием равновесия как для системы (Ai) так и для системы (А) (Z является общей границей для областей G; и G, в которых соответственно определены системы (Ai) и (Aft)); в этом случае мы получаем склеенное состояние равновесия; простейшие примеры - склеенный фокус (рис. 188)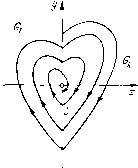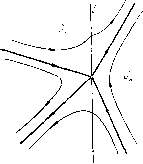

Рис. 188

Рис. 189

и склеенное седло рис. 189 (в обоих случаях траектории, стремящиеся к О и в области G< и в области G стремятся к О при

f-±oo);

аг) точка О является состоянием равновесия только для одной из систем (Ai) и (А), например для системы (Ai); тогда к такому СОСТОЯНИЮ равновесия траектории в области G, для которой Дуга I также является граничной, могут стремиться («втыкаться») при конечных значениях t.

б) Точки дуги сшивания I, являющиеся точками стыка траекторий двух систем (Ai и (А) (определенных в областях G<