Тогда ири переходе от значений x <ко к значениям x > хо смена устойчивости фокуса может осуществляться без рождевия предельного цикла. Простейший пример такой бифуркации дает линейная система вида

х = а(х)х + (х)у,

у = -(х)х + а(х)у {{х)фо ири \х~хо\ <бо).

Если: ири х<.хо а(х)<0; ири х = хо а{хо) = 0; ири х>хо, а(х)>0, то мы, очевидно, получаем смену качественных структур, представленную на рис. 106, и очевидно, без рождения предельного цикла.

VI. Рассмотрим случай разделения сепаратрисы без рождения предельного цикла, когда значению параметра x = хо соответствует консервативная система.

Пусть при х = хо y системы (Ах) сепаратриса l седла 0(хо) образует петлю, причем все траектории в окрестности петли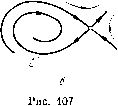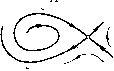

замкнуты (рис. 107, а). (В этом случае, очевидно,ас==/х(Ж(,, i/q)-Ь

+ Qy{Xo,yo) = 0.)

Тогда возможна смена качественных структур, представленная на рис. 107 (ири х<хо и х> хо сепаратрисы L и L" (рис. 107, б) и соответственно l* и l** (рис. 107, в) различно расположены, но при этом ни ири x < хо, ни ири х> хо не рождается предельный цикл).

§ 3. Случай, когда правые части зависят более чем от одного параметра. В случае, когда правые части динамической системы зависят более, чем от одного параметра, каждая из указанных в § 2 последовательных смен качественных структур будет происходить ири изменении параметров вдоль дуги, пересекающей в пространстве параметров негрубую п - 1-мерную пленку, точкам которой соответствуют системы первой степени негрубости с одним из негрубых особых элементов типов I-IV § 2.

Пусть, например, /г = 2, т. е. правые части системы (Aj.) зависят от двух параметров xi и х2, и мы имеем плоскость параметров xl и 2.

Р(ж, г/. Я,, Я2)=0, Q{x, у,ХиХ2)==0,

A{x,y,Xi,X2)=

= 0. (1)

Исключая X ж у жз этих трех уравнений, мы получим одно соотношение между параметрами Я1 и Яг:

А*(Я1, Я2)=0.

Это соотношение дает уравнение бифуркационной кривой, неособым точкам которой (г. е. значениям (Я5, Яз) точек этой кривой, для которых (5А*/5Я1)2-1-(5А*/5Я2) 0) соответствуют системы (Ая,), имеющие двукратное состояние равновесия седло-узел.

Если у кривой А*(Я1, Я2)=0 есть особые точки, т. е. точки, в которых dA*/dKi = дА*/дХ2 = О, го эти точки соответствуют системе (А»,), имеющей состояние равновесия кратности выше второй. Если мы в пространсгБе параметров пересечем кривую А* = О, переходя с одной стороны этой кривой на другую, го на плоскости {х, у) для рассматриваемой динамической системы в окрестности седло-узла будет осуществляться смена качественных структур, рассмотренная в § 2 (см. рис. 99 гл. 10).

Рассмотрим еще другой случай системы первой степени негрубости, именно случай, когда система (А) имеет сложный фокус первого порядка, г. е. когда для рассматриваемой системы (AiJ вьшолняются условия

Р {х, у, Я,, Яг) = О, (х, у, Хи Яг) = О, о {х, у, Я, Яг) = Р; (х, у, Xi, Я2) + Qy {х, у, Х, X,) = О, (2)

Будем называть лпнпю в плоскости параметров Xi и Яг, все точкп которой соответствуют бифуркационным значениям параметров, бифуркационной кривой. Предположим, что для рассматриваемой динал1Пческой системы, правые частп которой зависят от двух параметров,

dx/dt = Р{х, у, Xi, Хг),

dy/dt = Q{x, у, Хи h),

точки бифуркационных кривых соответствуют системам первой степени негрубости (как указывалось, это должно иметь место в общем случае вхождения параметров в правые части).

Пусть, например, у системы (А) существует двукратное состояние равновесия седло-узел. Это означает, что рассматриваемая система соответствует значениям параметров Xi и Яг, которые удовлетворяют системе уравнений

И при ЭТОМ А (а;, у, Яь Я2)> 0. Исключая а; и г/ из трех соотноще-ний, мы, вообще говоря, получим одно соотношение между параметрами Х[ и Х2-

а*{ХиХ2)=0. (а*)

Точкам бифуркационной кривой а* = О (т. е. значениям Я? и Х1 для точек этой кривой) соответствуют системы (А».), у которых есть сложный фокус. Так как мы предположили, что бифуркационным кривым соответствуют системы первой степени негрубости, то при значениях Я° п Я", соответствующих кривой а* = = 0, Li¥= 0. Обычно по знакам да*/дХ[ и да*/8X2 можно установить, с какой стороны от кривой а* = О фокус устойчив, а с какой - HeycToii4HB. Если можно установить знак L[, то тогда мы можем различить, какая из смен качественных структур: случая Па, или Пб, имеет место при пересечении бифуркационной кривой.

Обратим внимание на следующее. Если исключить значения X, у из трех уравнений (2), не учитывая условия А{х, у, Х[, Я2)> > О, то мы получим кривую на плоскости (Я1, Я2)

а*(Я1, Я2)=0,

„ * * „ *

которая состоит пз двух частей и Oj; точки одной части

соответствуют системам (Аг.), имеющим сложный фокус, а другой части - Ог - системам, имеющим седла, в которых седловая величина

ас = 0.

Точки второй части сг* могут представить интерес для качественного рассмотрения системы (Ai). Действительно, значениям параметров по разные стороны от части соответствуют динамические системы, имеющие седла с различными знаками седловой величины Ос.

Если, кроме того, известно, что, как в области, где 0= > О, так и в области, где Ос < О, есть точки, которые соответствуют системам (Ai), имеющим сепаратрису, образующую петлю, то знание знака Ос, очевидно, позволяет судить об устойчивости или неустотиивости цикла, рождающегося из этой петли. Примеры использования сведении о знаке Ос даются в задачах ч. П1 и IV.

Методы нахождения (аналогичные методам нахождения кривых а = 0 и А = 0) уравнени!"! бифуркационных кривых, соответствующих двукратным циклам или сепаратрисам, идущим из седла в седло, очевидно, отсутствуют. Действительно, для того чтобы методом, аналогичным методу определения кривых А* = О и а* = О, найти уравнение бифуркационной кривой, соответствующей двукратному предельному циклу, нужно, очевидно, najiTH решение, соответствующее предельному циклу (соответ-