Для исследования особых точек (состояний равновесия) удобно перейти к полярным координатам. Получим

Особые точки - точки пересечения изоклин

dp/d(p = 0, Лг/ + р2(1-р2)=0, d(p/dt = 0, Ах + ар = 0.

(7) (8)

Кривая (7)-изоклина в полярной системе координат - легко может быть построена. При О < < 4/27 она состоит из двух

Устойчибый узел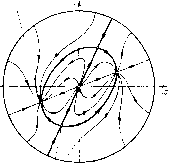

Седло Неустойчивый узел

Рис. 130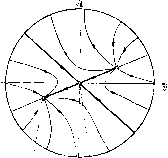

Устойчивый узел Сед "о

Рис. 131

симметричных относительно оси у замкнутых ветвей, охватывающих одна другую (сплошные замкнутые кривые на рис. 133). Кривая (8)- окружность радиуса Л/(2а), касающаяся оси у в начале координат (штриховые линии на рис. 133 соответствуют трем различным значениям а). Возможны три точки пересечения изоклин (8) и (7) (точка р = 0 исключается): две с внешней ветвью (7) и одна с внутренней (см. рпс. 133). С возрастанием параметра а точки пересечения внешней ветви (7) с окружностью двигаются навстречу друг другу и затем при а = ai сливаются; при дальнейшем возрастании а эта точка исчезает.

Пусть А фиксировано и выбрано так, чтобы кривая р = 1/У2 отделяла внешнюю часть кривой (7) от внутренней, не пересекаясь с ними. Это возможно сделать, так как при Л О внутренняя ветвь стягивается в точку а; = г/ = О, а наружная превращается в окружность р = 1. При таком выборе А величина

+ = 2 (1 - 2р2) (9)

меняет знак как раз на кривой р = 1/У2 и, следовательно, будет

положительной для особой точки на внутренней ветви кривой (7) и отрицательной для особых точек на внешней ветви.

Возьмем в качестве топографической системы Пуанкаре семейство окружностей х + у = С и составим производную dCldt вдоль траекторий системы

dC 2х + 2у = 21Ау + рЦ1 -

Как видно, производная dC/dt меняет знак на кривой (7). Две крайние кривые топографической системы, касаюш;иеся контакт-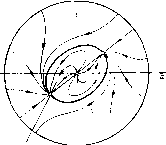

Рис. 132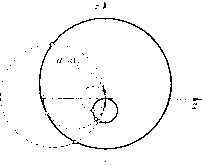

Рис. 133

Ной кривой (изоклины (7)), образуют кольцо, на внешней и внутренней границе которого производная dC/dt имеет разные знаки. Очевидно, что при больших р будет dC/dt < 0. Таким образом, на внешней границе кольца dCjdt < О, а на внутренней dCjdt > 0. Через обе границы траектории входят внутрь кольца. Особая точка на внутренней ветви кривой (7) лежит внутри цикла без контакта, ее индекс Пуанкаре, следовательно, равен + 1, и точка может быть лишь узлом либо фокусом. Так как для нее выражение (9) положительно, то фокус или узел неустойчивы. Две другие точки лежат в кольце между циклами без контакта, следовательно, сумма индексов этих точек равна нулю, и

одно из них седло. Вторая точка устойчива, так как для нее выражение (9) отрицательно.

Проследим изменение качественной структуры траекторий в зависимости от параметра а. При я = О прямая а; = О будет интегральной кривой. Качественная картина траекторий определяется однозначно и будет такая, как на рис. 134.

Рис. 134

При возрастании а точки (седло и устойчивый узел) будут сближаться, но до момента слияния качественная структура не может измениться, так как не меняются число и характер особых точек и поведение сепаратрис и так как внутри кольца не могут возникнуть предельные циклы за счет сгущения траекторий. Последнее невозможно, потому что кривая Рх + Qy = О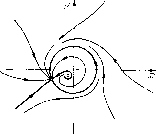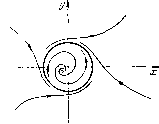

Рис. 135

Рис. 136

лежит вне кольца (критерий Дюлака). При дальнейшем возрастании а точки сливаются и затем исчезают.

Из особой точки седло-узел и сепаратрисы седло-узла (см. гл. 10, 11) рождается единственный (так как Px + Qy¥=0 в седло-узле) предельный цикл (рис. 135 и 136).

§ 3. Некоторые простые примеры динамических систем на цилиндре. В дальнейшем мы подробно остановимся на качественном исследовании классического уравнения движения самолета в вертикальной плоскости [45, 42, 75, 148], которое после надлежащей замены переменных и параметров может быть записано в виде системы

d(f)/dt = р - cos ф, dp/dt = 2р (Я. - рр - sin ф)

(Я и р - положительные параметры). Следующие примеры посвящены рассмотрению частных случаев этого уравнения. Пример 1.

d(f/dt = р - cos ф = Р, dp/di = 2р (Я - sin ф) =

(эта система получается из системы (1) при р = 0). Будем рассматривать только часть фазового цилиндра, соответствующую (что соответствует смыслу этих переменных) р > 0. а) Я = 0. В этом случае мы получаем систему

d(f/dt = р - cos ф, dp/dt = - 2р sin ф