хК2/о) Ру(\Уо)

(J = Рх{ХоУо) + Qy {о, У о)-

Теорема 1. Если система (А) является системой первой степени негрубости в замкнутой области G, то она не может иметь в G состояния равновесия, для которого А = О и а - О.

Всегда можно считать, что жо = j/o = О, и тогда систему (А) в окрестности состояния равновесия, для которого А = О, аФО, можно привести линейной заменой переменных к виду

х=Р2{х,у), y==by + Q2{x, у),

Pzix, у) U Q2{x, у)-функции, разложение которых по степеням хну начинается с членов не ниже второй степени.

Теорема 2. Если система (А) является системой первой степени негрубости в области G, то в G у нее не может быть состояний равновесия, у которых А == О, аФО, 2(1, 0) = 0.

Состояние равновесия, для которого А = О, аФО, Piii, 0)= = 1оФО, является седло-узлом).

Геометрически это состояние равновесия имеет вид, представленный на рис. 51, гл. 4.

Отметим, что седло-узел есть двукратное состояние равновесия (см. § 3 гл. 10).

Рассмотрим теперь состояние равновесия О, для которога А > О, 0 = 0, т. е. состояние равновесия, уже изучавшееся в § 5 гл. 3, которое может быть либо фокусом, либо центром. Как мы видели в § 5 гл. 3, в окрестности этого состояния равновесия на некоторой части полупрямой, примыкающей к точке О, можно

) Кроме седпо-узла, на плоскости других двукратных состояний равновесия нет.

Мы сформулируем здесь основные предложения, с помош;ыо которых устанавливаются необходимые и достаточные условия того, что спстема (А) является системой первой степени негру-бостц в G.

Необходимыми и достаточными условиями грубости динамической системы являются условия I-III § 6 гл. 8.

Следовательно, если система (А) является негрубоп, то у нее непременно должны существовать:

1) либо состояние равновесия, у которого Д = 0;

2) либо состояние равновесия, у которого А > О, о = 0;

3) либо предельный цикл с характеристическим показателем, равным нулю;

4) либо сепаратриса, идущая из седла в седло.

§ 3, Состояния равновесия, возможные в системе первой степени негрубостп. Сохраним обозначения:

[х (Ф {Г), г) (fy) + (Ф (О, г) (fy) ] Л = О,

т. е. }i\ = \. и одновременно h2 = 0.

Замкнутая траектория, для которой h = 0 (т. е. fti = 1) и ЛгтО, называется двойным {двукратным) предельным циклом (этот цикл очевидно является полуустойчивым) (рис. 65 гл. 5).

§ 5. Условия на сепаратрисы седел и седло-узлов в системе первой степени негрубости. Пусть теперь у системы (А) существует сепаратриса, идущая из седла в седло. Рассмотрим, в частности, тот случай, когда сепаратриса Ьо идет из седла О в то же седло. Тогда Ьо вместе с седлом О образует простую замкнутую кривую Со. Мы будем говорить в этом случае, что сепаратриса образует петлю или что мы имеем петлю сепаратрисы. Если прн этом сепаратрисы седла О, отличные от Lo, лежат внутри петли (внутри Со), то мы будем говорить, что Lo образует большую петлю. Укажем следующие основные свойства петли сепаратрисы.

построить функцию последования

г = /{•о) = "i-o + "г-о + ccrt + ...

в случае, когда о = О, ai = 1 и «г = 0.

Теорема 3. Если система (А) является системой первой степени негрубости в области G, то в области G не может существовать состояние равновесия, для которого А > О, 0 = 0 и аз = 0.

§ 4. Замкнутые траектории, возможные в системе первой степени негрубости. Перейдем теперь к выяснению вопроса о том, какие замкнутые траекторхш возможны в системе первой степени негрубости. Пусть Lo - замкнутая траектория, x = (f(t), y = {t)-соответствующее ей решение. Пусть

s = his + h2s + hss +...

- функция последования, построенная в окрестности Ьо на некоторой дуге без контакта, проведенной через какую-нибудь точку Ьо.

При этом, как мы видели,

К = е\ Л = -i- j (ф (t), г) (t)) + Qy (ф (t), (t))] dx. о

Теорема 4. Если система (А) является системой первой степени негрубости в G, то в G не может существовать замкнутая траектория, у которой

1. Если в седле 0{хо, уо) величина

ас = рх (Жо, у,) + Qy (Хо, у о) > О,

то петля неустойчива (т. е. все траектории, проходящие через достаточно близкие к ней точки, лежащие внутри нее или со-соответственно вне ее, стремятся к петле при i->- -<»). Если величина

ас = Рх (Жо, Уо) + Qy {Хо- Уо) < О,

то петля устойчива (см. рис. 96 и 97).

2. Если в седле

Рх{ХоУо) + QyiXoyo) = 0,

то возможен как случай, когда петля устойчива, так и случай, когда петля неустойчива, а также случай, когда все траектории.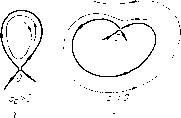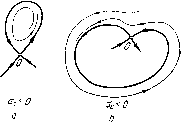

Рис. 96

Рис. 97

проходящие через точки внутри (вне) петли, достаточно близкие к петле, замкнуты.

Теорема 5. Если система (А) является системой первой степени негрубости в G, то в G не может существовать сепаратриса, идущая из седла в то же седло, если в этом седле К (Xq, Уо) + Qy {Xq, z/o) = О {хо, у о - координаты седла).

Величина ас = Рх (Жц, у) + Qy {х„, у) {0{х, у) - седло) называется седловой величиной.

§ 6. Необходимые и достаточные условия первой степени негрубостп. Назовем независимой особой траекторией первой степени негрубости каждую из траекторий следующих типов:

1) состояние равновесия седло-узел, для которого А=0, 0=70, Р2(1, 0)Ф0 (см. § 3);

2) сложный фокус первого порядка (о = О, Li = a3=r0) (см. гл. 3, § 5);

3) двойной предельный цикл {h = 0, h20) (см. § 4);

4) сепаратрису, идущую из одного седла в другое;