4. ц = 1. Консервативный случай изображен на рис. 83. Для всех Я>0 единственно возможной будет картина, изображенная на рис. 88.

СеЗло-узел

Ссдла-узел

Устойчивый фокус (узел)

Уло-узел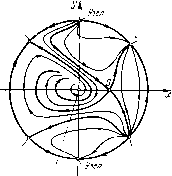

Ц Узел

СеЭпо-изел

Седло-узел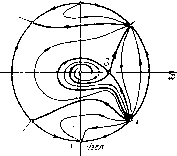

Рис, 88

Седпо-узел Седло-узел

Устойчивый фону с (узел)

Рис. 89

едло-узел

5. ц > 1. Консервативный случай изображен на рис. 84. Для малых значений Я,>0 качественная картина изображена на рис. 89. (В общей случае, аналогично случаю О < ц < 1, качественная структура определяется неоднозначно, см. § 2 гл. 14.)

ЧАСТЬ II ТЕОРИЯ БИФУРКАЦИЙ

ГЛАВА 7

ДВУМЕРНЫЕ КОНСЕРВАТИВНЫЕ СИСТЕМЫ. НЕКОНСЕРВАТИВНЫЕ ДИНАМИЧЕСКИЕ СИСТЕМЫ ТЕОРИИ КОЛЕБАНИЙ. ОБЩИЕ ТЕОРЕМЫ

Введение. Качественная теория дифференциальных уравнений, в прошлом столетии вызванная к жизни задачами небесной механики, получила в начале нашего столетия новый мощный стимул к развитию в связи с задачами радиотехники, радиофизики и вообще в связи с развернутым рассмотрением колебаний- в частности, автоколебаний - во всевозможных областях физики и техники. Качественная теория дифференциальных уравнений стала неотъемлемой частью математического аппарата теории колебаний. Однако характер динамических систем, возникающих при рассмотрении задач теории колебаний, оказался существенно отличающимся от характера динамических систем классической небесной механики. Поясним в общих чертах, в чем заключается указанное различие.

Как задачи небесной механики, так и задачи теории колебаний существенно нелинейны. Но в то время как динамические системы небесной механики являются гак называемыми консервативными, в частности, гамильтоновымп системами, динамические системы теории колебаний заведомо не являются такими системами. Для того чтобы отчетливо уяснить это различие, укажем, не давая точных определений, некоторые характерные особенности консервативных систем.

§ 1. Свойства консервативных систем на плоскости [2, 3].

Как и всюду, мы предполагаем правые части динамической системы аналитическими функциями.

Простейший случай консервативно!"! системы-это гамильто-нова система, т. е. система, имеющая вид

х = дн/ду, у = -дН1дх, (Н)

где Н{х, г/)-аналитическая функция переменных х ж у. Система (Н) очевидно имеет аналитический интеграл

Н{х,у) = С

{интеграл энергии). При этом:

§ 1]

СВОЙСТВА КОНСЕРВАТИВНЫХ СИСТЕМ НА ПЛОСКОСТИ

а) в оистеме (Н) возможны простые состояния равновесия (см. гл. 3) лишь типа центра и седла;

б) в системе (Н) замкнутые траектории (соответствующие периодическим решениям этой системы) не являются изолированными, а заполняют целые области.

Отметим еще следующее характерное для гамплыоновых систем свойство.

Выделим на плоскости {х, у) область Оо, ограниченную простой замкнутой кривой, не содержащую состояний равновесия. Площадь этой области может быть записана в виде

пл. Оо = J 1" dx dy„.

Рассмотрим траектории, при t = Q проходящие через точки области Оо

х = ф(г; Хо, уо), y = {t\XQ,ya),

и возьмем область а, которую при некотором фиксированном t = x заполнят эти точки. Нетрудно показать.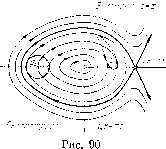

что мы имеем

пл. or = J j" Д dxdy.

dyldx ду/ду

= 1,

о """0

и что при этом область а имеет ту же площадь, что и область Оо (рис. 90):

пл. а = пл. Оо.

Это утверждение носит название теорема Лиувилля.

Консервативной системой мы будем называть систему

dx/dt = Р{х, у), dyldt = Q{x, у),

определенную в некоторой области плоскости G пли на всей плоскости, которая после умноженпя правых частей на интегрирующий множитель М{х, у), являющийся аналитической функцией, не обращающейся в нуль во всей области определения системы (1), и после изменения параметризации может быть приведена к гамильтоновому виду (Н):

dxldx = M{x, у)Р{х, у) = дН/ду, dy/dx ==М{х, y)Q{x, у) = -дН/дх, dx = dt/M{x,y).