предельные циклы, схватывающие цилиндр соответственно в верхнем и нижнем фазовых полупространствах, будут «влипать» в сепаратрисы, идущие из седла в седло.

На плоскости (D) (р -2 -л/2 = 0) предельный цикл, охватывающий состояние равновесия Oi ([4-0/2, 0), «влипает» в сепаратрису, идущую из седла в то же седло (рис. 201, 4.6). На поверхности (Е) (1 -2р/л = 0) в точке 01(1x0/2,0) система имеет состояние равновесия типа центра (рисунок не приводится).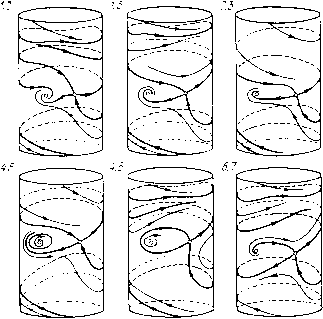

Рис. 201

На рис. 201 изображены качественные картины фазовых траекторий, соответствующих бифуркационным значениям параметров; указываются номера тех областей, на границе между которыми система (1) имеет указанную качественную картину фазовых траекторий.

§ 2, Автоподстройка при кусочно-постоянной аппроксимации характеристики.

1. Рассматривается система на цилиндре dy

=у-(ф)-2ар

1 =

(ф) = (ф + 2л).

при аиироксимации (ф) кусочно-постоянной функцией

(-1 при - я<ф<0,

при о<;ф<;я.

По физическому смыслу параметров: а > о, > о, > 0. Система не определена при у = 0, = 0.

Введем малый положительный параметр р, полагая а = рао, Y = pYo, и перейдем к системе

dy/dt = F (ф) + р (Vo - 2a,f,yly + f,%

dp/dt = y.

При p = 0 система имеет интеграл Я(Ф, !/)= -я + = h.

- я < ф < О, 0< ф<я.

Будем искать предельные циклы, охватывающие цилиндр в верхнем фазовом полупространстве. Замкнутые кривые семейства Н(ц>, у) = h при 0<h<oo охватывают фазовый цилиндр. Вблизи интегральной кривой Ch консервативной системы (при р = 0) имеется предельный цикл системы (1), если ho будет корнем уравнения

i(o)- \ (yo-2ao~)d = 0.

Интегральная кривая Ch, проходящая через точку М{-п,уо), состоит из двух кусков С- и С+:

Вычисляя интеграл, получим "У2я + 2h

Ч)1(/1) = 2яуо-4аоР

- arctg

y2n + 2h

i"!--arctg у]]<2яуо

(выражение в квадратных скобках всегда положительно, так как /(а;) = а; -arctga; > о, если ж>0, и /(a;i)>/(а;о), если х\>хо),

У2л + 2h УШь

1iW = -4aoP

Р"! + 2я -Ь 2h + 2h

= -4/2яа„р

- 2 У/г (я + h)

(Р + 2h) if + 2П + 2h) (У + УК)-26 н. Н. Баутин, Е. А. Леонтович

Из (2) и (3) находим

г),(0) = 2луо-4аор

arctg 2л Vo,

4 l/2iia„B г);(оо) = Ит ij);(/i) = 0.

h-oo

Производная ifii(/i) обраш;ается в нуль нри условии Функция ifii(/i) имеет единственный минимум

ij5i,mm== 2луо -4аор

п + h

= 8,

Ф (z) == z* - arctg z/* > О,

и единственную точку перегиба, соответствуюш;ую обращению в нуль второй производной:

r2 2и 2h

y-2h

\ У 2л + 2h if + 2п + 2hf У2к if + 2hf j

-4aoP [Ii{h)-IM-Функции 1 и 2, как легко проверить, состоят из двух монотонных ветвей (имеют единственный минимум) и получаются

одна из другой сдвигом на 2л по оси h. Их точка пересечения (очевидно, единственная) соответствует корню уравнения {К) = 0.

График функции (й) имеет вид, представленный на рис. 202.

Из (5) очевидно, что, распоряжаясь величиной положительного параметра «о, можно реализовать случаи, когда кривая ifii(/i) целиком расположена выше оси /г., когда она касается оси h и когда пересекает ось h.

Касанию (ifii,miii(/2<)) = 0) соответствует рождение иолуустой-чивого предельного цикла из сгущения траекторий. Бифуркационная кривая (поверхность) для этого случая дается уравнения-

Рис. 202