
 |
|
Главная страница Приемы качественного исследования [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [ 89 ] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] ИЗ (25) полулаем Ч;(1)= + оо, d + l>0, Ч;(1) = 16Яо, d+l = 0, <(1) = -о°, d + KO. (26) Покажем, что может иметь не более одного экстремума (максимума). Это будет следовать из того, что при условии Wi{Ko) = 0 будет всегда 4i(>Co)<0. Из (16), (17) видно, что liXo) обращается в нуль при значении d= - {2-1) F-2E Для (Ио) из (18) и (27) находим 16xji?-(l-x)1 4iK) = - <о, (27) (28) так как выражения в квадратных скобках положительны в интервале О < >с < 1 (приложения I и II). Сопоставляя (23), (26) и (28), заключаем, что при d + 1 >0 функция 4i(>c) будет монотонной (возрастающей); при d+\< < О она будет иметь один максимум. Возможные типы поведения функции представлены на рис. 142. Если d+l>0 и 4i(l)>0, то существует единственный корень >с = >ci функции 4i(>c), соответствующий предельному   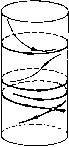 Рис. 142 Рис. 143 Рис. 144 пиклу, охватывающему верхний фазовый полуцилиндр (устойчивому, так как 2/l(Xi)>0). Если при этом d -3<0, то из (24) следует, что при возрастании %о значение может стать отрицательным, и тогда функция 41 (>с) корней иметь не будет. Значениям параметров, при которых 41 (1) = о, соответствует стягивание устойчивого предельного цикла к петле сепаратрисы седла, охватывающей верхний фазовый полуцилиндр (рис. 143). Если d+i<0 (и, следовательно, d -3<0), то при 4i(l)> >0 опять существует единственный корень но теперь функция 4i(>c) имеет одпн максимум и при перемене знака %i(l) (при возрастании Ко) из точки х = 1 появляется второй корень функции W[{k), соответствующий неустойчивому предельному циклу на верхнем фазовом полуцилиндре. На верхнем фазовом полуцилиндре будет два предельных цикла (рис. 144). При дальнейшем возрастании X эти циклы сближаются, сливаются в двойной (полуустойчивый) и затем исчезают. Бифуркационная кривая, соответствующая существованию двойного цикла, определяется условиями илп в параметрическом виде d = ->c2F/Oi, Яо = 2л-(о/Фо, (29) где Фо п Oi - то же, что в (13) и (17). Нетрудно обнаружить, что бифуркационная кривая двойных циклов (28) прп нО уходит в бесконечность (прямая Яо = О будет асимптотой), а при х1 имеет предельную точку d = -i, Яо = Зяуо/16, расположенную на бифуркационной кривой петель сепаратрис ¥i(l)2n7o + Xo(d-3) = 0. (30) 2. Бифуркации, связанные с поведением функции ("><). Для Ч2(х) из (13) имеем 2(0)=+«>, (31) 42(1)= 2яТо - (8/3)Яо(й - 3). (32) Из (16) видно, что iiK) отличается от 4i(x) только знаком. Поэтому в силу (26) будет Ча(х) = + оо при d + КО. Кривая Win) будет иметь экстремум (минимум) лишь для отрицательных значений d, но из (13) непосредственно обнаруживается, что в этом случае 42 (с) обращаться в нуль не может, так как квадратная скобка в (13) положительна (приложение III). Функция 42(х) будет иметь единственный корень, соответствующий устойчивому предельному циклу, охватывающему нижний фазовый полуцилиндр, если Ч2(1)<0. Из условия 42(1) < О вытекает, что d - 3>0 и, следовательно, выражение (33) при убывании % может менять знак. Обращению в нуль величины W2{1) при убывании X соответствует стягивание устойчивого предельного цикла к сепаратрисе седла, охватывающей нижний фазовый полуцилиндр (рис. 145). 3. Бифуркации, связанные с поведением функции Ч!з(х). Перейдем теперь к рассмотрению предельных циклов, рождающихся на кривых центра. Из (15) непосредственно обнаруживается, что при d<0 функция Чз(><) обращаться в нуль не может, так как выражение в квадратных скобках в (15) положительно (приложения I и IV). По критерию Бендиксона при О < d < 1 циклов нет {Pv + Су о), поэтому Чз(><) при О < d < 1 корней также не имеет. Проследим поведение Чз(>) при d 1. 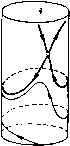 Рис. 145 Из (15), (19) и (20) получаем 43(0) = О, 43(1) = - Я(d-3), Ч;(0) = 0, Ч;(1) = -оо, (0) = 8лЯ(й -1). (33) (34) (35) Из (34) и (35) следует, что при любых положительных d> i у кривой W%{x) в интервале О < >с < 1 существует по крайней мере один экстремум. Нетрудно убедиться, что экстремум (максимум) может быть только один. Мы будем иметь, очевидно, Чз (>С(,) = О, если Хо такое, что обращается в нуль выражение в квадратной скобке в (19), т. е. если =-2>1- (36) Нетрудно видеть, что при условии (36) будет 16Х, 2 ЧзК) = 1-2 2E-F 2 (1 - х?) EF-{\- х?) - Е] < О, так как квадратная скобка знака не меняет (дискриминант отрицателен) и 2Е - F >0. Так как Чз(Х(,)<;О, то экстремум кривой Чз(х) является максимумом. Вид кривой при различных d приведен на рис. 146. При d > 3 кривая не пересекает ось х - циклов нет. При d = 3 будет 43 (1)= О, Чз(1) = - оо - это соответствует возникновению предельного цикла, охватывающего состояние равновесия. При [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [ 89 ] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] 0.0116 |