ничена сверху функцией т = т(ц), соответствующей любому и, фиксированному на интервале гр < м < - у), а предел этой ограничивающей функции при ц->-0 может быть сделан как угодно близким к нулю, если взять и достаточно близким к г(Р - у).

Приложение П. При < м < г(Р - у). Это предельное значение находится непосредственной подстановкой предельного значения т(х). Если мг(Р - y), то положим в равенствах (4) х =шт. Первое из них при фиксированном и и малых ц определяет функцию х = такую, что

lim X = 4 In-iri-г-

(Доказательство аналогично доказательству в приложении I.) Положим теперь во втором из равенств (4) х = х(ц) и найдем, что при х->-0 будет limy[x(n), И = "-•(P-T)• Пpимep 3. Пусть Р(ф)-функция периода 2я такая, что I- 1 при - я<ф<0, (ф) = I 0<ф<л.

Схема доопределенных движений по прямой ф = я приведена на рис. 225, а (здесь масштаб по оси у уменьшен в 2h раз). Изображающая точка, попавшая в точку (я, у), где у>2Ъ, совершает скачок величиной 2Ь вниз по прямой ф = я, после чего продолжает движение при ф > я в соответствии с системой (2). Если Ь(1 - -R)<у <2Ъ, то изображающая точка перескакивает в точку (я, 0) и находится в ней в течение времени b{l + Q)

2bk\n

y-b{l-Qy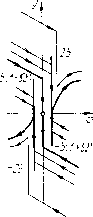

после чего продолжает движение при ф > я в соответствии с системой (2). Если y = b{i - Q), то изображающая точка перескакивает и точку (я, 0) и остается там неограниченно долго. Если 0<1/<Ь(1 - Q),To изображающая точка перескакивает в точку (я, 0) и находится в ней в течение времени

6(1-0)

Рис. 225

26/1 In

после чего продолжает движение при ф < я. Поведение изображающей точки, попавшей на прямую ф = я в нижнем полуцилиндре, аналогично (нужно поменять у на и Q на -Q). 28*

Точка (я, 0) будет состоянием равновесия, аналогичным седлу, а траектории, проходящие через точки [я, 6(1 -Q)] и [я, - b(l + Q)]-его сепаратрисами. Роль двух других сепаратрис выполняют траектории, выходящие из точки (я, 0).

Схема догахределенных движений по прямой ф = 0 приведена на рис. 225, б. Изображающая точка, попавшая в точку (О, у), где у > О, совершает скачок величиной 26 вверх по прямой ф == О, после чего продолжает движение при ф > О в соответствии с системой (2). Если у<0, то изображающая точка совершает скачок величиной 26 вниз по прямой ф = О, после чего продолжает движение при ф<0 в соответствии с системой (2). Точка (О, 0)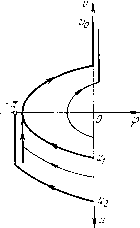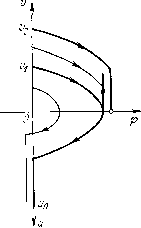

"о

2 и

Рис. 226

будет состоянием равновесия, аналогичным неустойчивому узлу. Из него выходят траектории, проходящие через точки (О, у), где О < i/ < 26 или -26 < i/ < 0. (Вертикальный участок такой траектории от точки (О, 0) до точки (О, у) изображающая точка проходит скачком.)

Когда система доопределена на прямых ф = О и ф = я, можно проследить любое ее частное решение на любом отрезке времени

и провестп ее качественное исследование. Исследование сходно с исследованием в примере 1, поэтому ограничимся лишь изложением результатов, относящихся к предельным циклам, охватывающим состояние равновеспя.

Возьмем на прямой ф = О две полуоси: полуось и - вниз от начала координат и полуось v - вверх от начала координат. На рис. 226 сверху изображены траектории, осуществляющие отображение v{u) части полуоси и в полуось v (слева), и траектории, осуществляющие отображение и (и) части полуоси v в полуось и (справа). Графики функций v{u) и и{и) приведены на том же рис. 226 внизу. Для и < ui функция v{u) находится обычным способом, только с учетом того, что все v нужно сделать больше на величину скачка. Участок ui < и < U2 весь переходит в одну точку Уо. Для этих и имеем и(и)= const = vq. Аналогичные соображения можно высказать о функции u{v).

Цикл соответствует точке пересечения линий v{u) и u(v). На рис. 227 показано изменение взаимного положения линий при изменении параметров. На рис. 228 - соответствующие превращения предельного цикла (соответствующие одна другой картинки на рис. 227 и 228 обозначены одинаковыми буквами). Очевидно, так же, как и в примере 1, расположение траекторий рис. 228 может быть изображено на цилиндре.

Для некоторой области в пространстве параметров линии имеют точку пересечения на кривых участках (рис. 228, а). Цикл не имеет кусков на прямых ф= -л и ф = л. При соответствующем изменении параметров точка пересечения передвинется в точку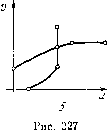

излома линии u{v). При этом цикл коснется прямой ф = л. При дальнейшем изменении параметров точка пересечения переходит на вертикальный участок линии (рис. 228, б). При этом на цикле появляется вертикальный участок на прямой Ф = я, который изображающая точка проходит скачком, после чего некоторое время стоит в точке (я, 0), прежде чем продолжит движение по циклу. В зависимости от дальнейшего изменения параметров возможны превращения двух типов: 1) концевая точка линии и{и) попадает на кривой участок линии v{u). При этом цикл влипает