
 |
|
Главная страница Приемы качественного исследования [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [ 26 ] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] уравнения равны бесконечности, и мы получаем два возможных направления: я/2 и Зя/2. Каждая траектория системы (16) стремится к состоянию равновесия О в определенном направлении, именно либо в направ- 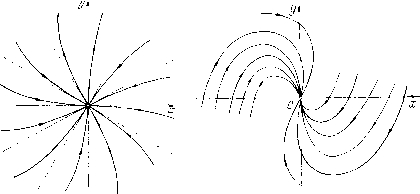 Рис. 42 Рис. 43 лении я/2, либо в направлении Зл/2; при этом имеется бесчисленное множество полутраекторий, стремящихся к О как в том, так и в другом направлении (рис. 43). 2. Характеристические корни действительны и разных знаков. Канонический вид системы: dxldt = kxx- {х, у), dy/dt Х2У + {х, у), %iK2 < 0. Уравнение (13) (как и в случае 1) имеет один нулевой корень и один, равный бесконечности. Пусть Xi < О, > 0. Траектории (полусепаратрисы седла) стремятся к седлу О в направлениях л/2 и Зл/2, О и л. При этом две полусепаратрисы стремятся к О при t -оо соответственно в направлениях я/2 ii Зл/2, две при t +00 в направлениях О и л. Во всех проведенных рассмотрениях мы предполагали, что система приведена к каноническому виду, и поэтому направления, в которых полутраектории стремились к состоянию равновесия, совпадали с направлением осей координат. Очевидно, для системы, не приведенной к каноническому виду, направления могут быть любыми в зависимости от коэффициентов системы. В случае фокуса, простого или сложного (т. е. когда характеристические корни комплексные или чпсто мнимые), корни уравнения (13) тоже комплексные, т. е. нет направлений, по которым траектории могут стремиться к состоянию равновесия. Как мы видели в § 5, в этом случае траектории - спирали. = Х2 - оХ + А = о (17) - характеристическое уравнение этого состояния равновесия. Для простого состояния равновесия по самому его определению А =7 О, т. е. корни уравнения (17) - характеристические корни - отличны от нуля. Уравнение, определяющее направления, по которым траектории стремятся к состояниям равновесия: Ру {х„ г/о) к - {Qy -Р.)к + <?; (Хо, г/о) = 0. (18) Корни Xi и Хг характеристического уравнения (17) и корни ki и Аг уравнения (18) связаны соотношениями , К-РЛо У о) , К-РЛ\Уо) гь-\ - -.-, /to - -;-• (Vo) Ру(-У) Очевидно, корни к\ и А;г действительны тогда и только тогда, когда действительны Xi и Хг. В зависимости от того, каковы характеристические корни состояния равновесия, система может быть в окрестности этого состояния равновесия приведена линейным преобразованием переменных к одному из следующих видов, которые называются каноническими (обозначения переменных сохраняются прежними) . 1. Характеристические корни действительны и различны (Xi =5Хг). Канонический вид системы: х = Х1Х + ф(х, г/), г/= Хгг/ + гз(х, г/). 2. Характеристические корни равны (Xi=X2 = X). Канонический вид системы: х = Хх +ф(х, г/), г/ = Хг/ + рх + гз(х, г/) (р может быть как равным, так и не равным нулю). 3. Характеристические корни комплексно сопряженные (Xi = а + Хг = а - i, 0). Канонический вид системы: x = ах-рг/ + ф(х, г/), у = <х + ау + {х, у). ) Состояния равновесия с чисто мнимыми корнями, рассмотренные в § 5, здесь, очевидно, не фигурируют. Можно показать, что в этом случае угол между положительным направлением касательной к траектории, стремящейся к фокусу, и положительным направлением оси неограниченно возрастает при t ->- +°°, если а < О (и при t-<», если а > 0). § 8. Сводка сведений о грубых состояниях равновесия Пусть 0{хо, г/о)-состояние равновесия системы (А), а выражения для А и о приведены в § 3 и 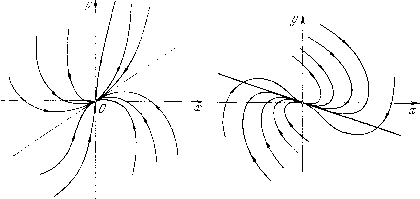 Рис. 44 Рис. 45 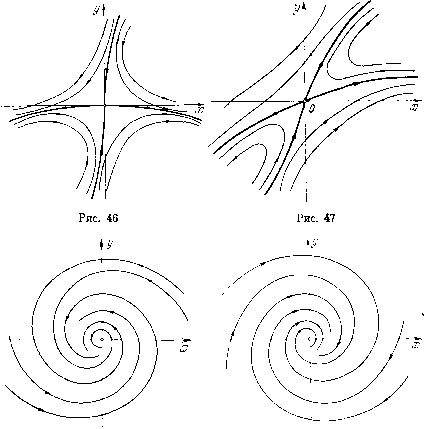 Рис. 48 в Н. Н. Баутин, Е. А. Леонтович Рис.-49 [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [ 26 ] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] 0.0106 |