
 |
|
Главная страница Приемы качественного исследования [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [ 141 ] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] (1 - е" + (1 + О) / \ \ COS т) + -- sin Г) \ 1 i/я- 8ШТ] (l + Q)e-lV(l-n) COS л --Г- sin ri SinT) Ее производные - du V ц = /я sin ne«V + . Асимптота - V = u + Al/nhu Введем параметр a In [ (1-Ь Q)/(l-Q) ], Для a>kin кривая u = u{v) изображена na рис. 220 вместе с ломаной (u - 2r при ы2г, = W«) = ( о при г(1-й)<ц<2г, являющейся графиком функции соответствия преобразования полупрямой Ф = я, у > О в себя, осуществляемого доопределенными движениями, и построенной ио формуле (7). На рис. 220 изображен случай, когда кривая и ломаная имеют общую точку на горизонтальном участке ломаной. Это означает, что на фазовом цилиндре имеется предельный цикл, при движении по которому изображающая точка имеет остановку в точке (ф = я, у = 0) на время, определяемое первой строкой формулы (6). Легко видеть, что цикл устойчив и что более одного цикла быть не может. При увеличении г точка иересечения кривой и ломаной попадает в начальную точку ломаной, что соответствует влипанию цикла в сепаратрису, образующую петлю (сепаратрису, идущую из состояния равновесия (я, 0) в то же самое состояние равновесия). Соответствующая бифуркационная поверхность в пространстве параметров г, hi, а имеет уравнения и{ц) = г(1 - й), Рассмотрим точечное преобразование полупрямой 7{ф = -я, = у > 0} в полупрямую С/{ф = я, у = и> 0), осуш;ествляемое траекториями системы (2). Если обозначить то при О <h\<i параметрические уравнения функции соответствия этого преобразования запишутся в виде v(r]) = 0. Исключив т), получим а = ki л - arctg \ 1 г + 2Упкг+п + -1п - При уменьшении г точка пересечения кривой и ломаной переходит на наклонный участок ломаной, чему соответствует превра-ш;ение «цикла с остановкой» в точке (я, 0) в «цикл без останов- 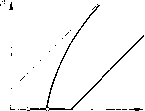 Рис. 220 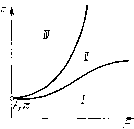 Рис. 221 ки». Поверхность, разделяющая в пространстве параметров области существования цикла с остановкой и цикла без остановки, имеет уравнение и{г\)=2г, i;(ti)=0. Их можно иереиисать так: У л sin ц (Ое 1 - (0 cos Г) - а = /cjT) - In (- cos т) - /ci sin ri) и рассматривать как параметрические уравнения сечения поверхности плоскостью hi - const. На рис. 221 приведено сечение пространства параметров плоскостью hi = const. В области / нет циклов. В области система имеет цикл с остановкой. В области / система имеет цикл без остановки. Качественная картина фазовых траекторий системы для случая цикла с остановкой приведена на рис. 222. Пример 2. Этот пример отличается от примера 1 знаками и г и иллюстрирует второй случай доопределения. Уравнения функции соответствия u = u{v), ее производных и асимптоты получаются из соответствующих уравнений примера 1, если считать hi = h{n + b) /Уя, = /1 -Ь fei, заменить Q на -Q, тригонометрические функции на гиперболические со сходным названием и поставить минус перед второй производной. Для получения всех значений v ж и нужн менять т) от О до оо, при этом V меняется от - оо до f = /я (1 - Q) (coj -t- hj), а и меняется от оо до щ = /л (1 + Q)(tOi - i), где и - 28 н. Н. Ваутин, Е. л. Леонтович отрезки, отсекаемые сепаратрисами седла (-лй, 0), соответственно от полупрямых V я и. Кривая uuiv) изображена на рис. 223 вместе с прямой v = и + 2г, являющейся графиком функции соответствия при преобразовании полупрямой ф = л, у > О в себя, осуществляемом доопределенными движениями. На рис. 223 изображен случай, когда кривая и прямая имеют точку пересечения. Это означает, что на фазовом цилиндре имеется предельный цикл. Легко видеть, что он устойчив и что более одного цикла быть не может. При уменьшении г прямая передвигается слева направо, и при некотором г точка пересечения 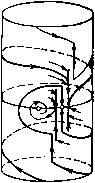 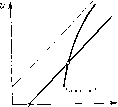 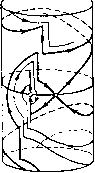 Рис. 222 Рис. 223 Рис. 224 попадает в точку При этом предельный цикл влипает в сепаратрису седла (-яО, 0), образующую петлю. Соответствующая бифуркационная поверхность в пространстве параметров г, hi, Q имеет уравнение = li + 2г или Q = - г/( j/ncoi) + hji. Качественная картина фазовых траекторий системы для случая, когда имеется предельный цикл, приведена на рис. 224. Приложение I. Пусть < w < г(Р - f). Функцию и = (т, р.), определяемую первым из равенств (4), не существующую при р, = О, доопределим ее пределом при ц -> 0. Получившаяся при этом функция , Г"(т, р.) при ц>0, Ь IP - 7 ехр {- т/г}] при fi = О удовлетворяет следующим условиям: 1) непрерывна, 2) если Хо = г X X In Inii? - и)], то /(То, 0) = и, 3) производная df/dx < 0. Следовательно, при зафиксированном на рассмотренном интервале и равенство и = f{x, ]i) определяет в некоторой окрестности точки (то, 0) од-йозначную непрерывную функцию х=х (р.) такую, что х (0) = т. А так как X (ц) = т« (р.) при х =?t О, то Итт(х) = То при х->-0. Пусть теперь иг(Р -7). Так как dujdx <Q, то функция T = T(i), соответствующая фиксированному на рассматриваемом интервале и, огра- [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [ 141 ] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] 0.0316 |