Мы получаем

У = Уо-

(10)

Полагая при О г/оДо°=с, мы получим параболы

у = сх

а при = О (когда выражение j/o/o" может не иметь смысла) - х = 0. При г/о = О мы получаем г/ = 0.

Перейдем от системы (8) к одному уравнению, например, записанному в виде dy/dx = by/ax или в виде

dx/dy = ax/by. (И)

Как было указано, уравнение (И) задает поле линейных элементов, и оно представлено на рис. 6. Если проинтегрировать

уравнение (И), то в качестве интегральных кривых в смысле § 10 мы получим параболы (10) и две оси координат.

Траекториями системы (8) являются те части (половины) парабол (10) и координатных осей х = 0 и г/ = О, на которые эти кривые разбиваются состоянием равновесия 0(0, 0). Из соотношений (9) видно, что если а < О, b <0, то точка на любой отличной от нуля траектории стремится к состоянию равновесия О при t +°°, а если а > О, 6 > О, то при t -> -оо. Напомним (см. § 5), что когда изображающая точка, двигаясь по отличной от состояния равновесия траектории L, стремится к некоторому состоянию рапновесия A(xq, г/о), то при этом всегда

t +°° или t ~оо

Таким образом, разбиение на траектории, определенное системой (8) (с указанными на траекториях направлениями)), имеет

) Если особых ЛИНИ11 нет, то для того, чтобы наметить направление па траекториях, достаточно наметить направление в какой-либо одной точке. Тогда во всех других точках направление определяется из соображений непрерывности. Определить же направление в какой-либо точке (хо, j/o), в которой Р{хо, г/о) ф О, можно, вычисляя в этой точке Р(ха, уа) и определяя в стой точке знак Р(хо, г/о); если Р{хо, уо) > О, то в точке (хо, Уо) dxIdt > О, а значит: вблизи этой точки при движении по траектории в сторону возрастания { -х возрастает, что и определяет направления на траектории, проходящей через точку {хд, г/о). Совершенно аналогично можно наметить направления на траекториях, рассматривая знак Q{xo, г/о) в точке, в которой Q{xo. Уо) Ф 0.

Рис. 6

вид, указанный на рис. 7. Состояние равновесия такого типа называется узлом, устойчивым в случае а < О, b < О (рис. 7, а) и неустойчивым в случае а > О, Ь > О (рис. 7, б).

Рассмотрим еще интерпретацию решений системы (8), т. е. интегральные кривые системы (8) в трехмерном пространстве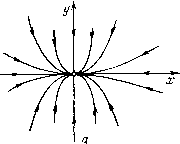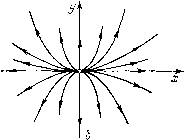

Рис. 7

(х, у, t). Из формул (9) следует, что интегральными кривыми системы (8) в пространстве {х, у, t) являются:

1) ось t, т. е. х = 0, у = 0 (эти уравнения получаются из уравнений (9) при хо = г/о = 0); она проектируется в состояние равновесия О фазовой плоскости;

2) показательные кривые

X = ХпС

У = 0,

расположенные в координатных полуплоскостях х>0, у = 0 или х<0, у = 0 и асимптотически стремящиеся к оси t при t +оо, если а < О, и при -оо, если а > 0; эти кривые проектируются в положительную и отрицательную полуоси абсцисс, являющиеся траекториями системы;

3) показательные кривые

аналогичные кривым типа 2);

4) кривые

расположенные на параболических цилиндрах у = сх" с образующими, параллельными оси t. Ось t разбивает каждый такой цилиндр на две «половины»; каждая интегральная кривая типа 4) лежит целиком в одной половине цилиндра и асимптотически

стремится к осп t при t -Ь<», если а < О, Ь<0, и при t->--оо,

если а > О, b > 0. Интегральные кривые типа 4) получаются друг из друга сдвигом вдоль оси t. То же справедливо для интегральных кривых типа 2) или 3).

Пример 4.

dxIdt = -у + ах, dy/dt = х + ay (12)

(а -отличная от нуля постоянная).

Векторное поле, определенное этой системой (при а<0), изображено на рис. 8. Решая систему (12) как линейную систему с постоянными коэффициентами, мы получим решение, соот-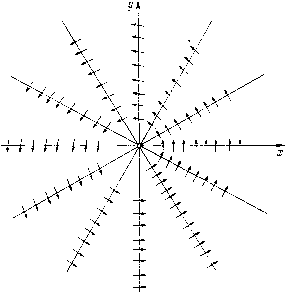

Рис. 8

вегствующее начальным значениям xq, уо, to в следующем виде {оно, очевидно, является функцией t - io в согласии с п. III § 3):

X = е" " [Хо cos (i - to) - у о sin {t - t)], у = Л"") [хо sin {t - to) + Уо cos {t - to)].

(13)

Характер траекторий рассматриваемой системы удобнее исследовать, переходя к полярным координатам. Мы получим после элементарных вычислений

dp/dt = ар, dQ/dt = 1. (14)

Решение этой системы

Р = Рое

= Q„ + t-to

(15)

является, очевидно, уравнением в полярных координатах траектории системы (12), проходящей при z = Хо через такую началь-