§ 5. Поведение сепаратрис седел в грубых системах. Теоремы 1-9 касаются двух типов особых траекторий: состояний равновесия и замкнутых траекторий. В настоящем пункте рассматривается последний тип особых траекторий - сепаратрисы.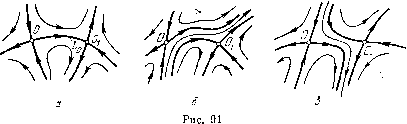

В грубых системах в силу теоремы 2, очевидно, возможны только сепаратрисы седел.

Если сепаратриса Lq седла О, стремящаяся к этому седлу, например, при t+°°, при t--оо также стремится к седлу (отличному от О или к тому же седлу О), то мы будем коротко говорить, что «сепаратриса седла О идет из седла в седло». Следующая теорема дает последнее необходимое условие грубости системы (А).

Теорема 10. 5 грубых системах не может быть сепаратрис, идущих из седла в седло (г. е. невозможны случаи, представленные на рис. 91, а; 92, а).

Для доказательства этой теоремы наряду с данной системой (А) рассматривается измененная Рпс. 92

система, дающая поворот поля,

т. е. система (Аа). Как мы видели (см. гл. 7), состояния равновесия системы (Аа) те же, что и у системы (А). Однако нетрудно показать, что сепаратриса состояния равновесия О системы (Аа) уже не идет из седла в седло («сепаратриса Lq разделяется» (рис. 91, б, в и рис. 92, б). Отсюда, очевидно, вытекает справедливость утверждения теоремы.

Следствие. В грубой системе сепаратриса не может быть предельной траекторией типа III § 5 гл. 2 (т. е. в грубой системе предельными траекториями могут быть только состояния равновесия (грубые) и предельные циклы (грубые)).

§ 6, Необходимые условия грубости. Достаточность этих условий для грубости системы. Объединение полученных результатов дает следующие необходимые условия грубости:

а) А =

= 0,

I. В замкнутой области G могут быть только грубые состояния равновесия, т. е. такие, для которых действительные части корней характеристического уравнения отличны от нуля. Это требование может быть сформулировано еще так: в области G не может быть состояний равновесия х = хо, у = г/о, для которых:

б) ири А > 0. [рх (а-о, г/о) + Qy {о Уо)] = 0.

II. В области G могут быть только простые (грубые) предельные циклы, т. е. такие предельные циклы, для которых характеристический показатель не равен нулю. Это требование может быть сформулировано еще и так: в области G не может быть периодических движений

= ф(0, y = {t) [(f{t + r) = (f{t), {t+x) = M{t)],

для которых

к = -[Рх{ц>(t), (t)) + Qy (ф(t), (t))] dt = 0. о

III. в области G не может быть сепаратрис, идущих из седла в седло.

В силу этих условий в грубой системе возможны особые траектории лишь следующих типов: грубые состояния равновесия, т. е. состояния равновесия узел, фокус и седло, простые (грубые) предельные циклы, сепаратрисы седел, в одну сторону стремящиеся к узлу, фокусу или к предельному циклу или ири некотором значении t выходящие из замкнутой области G.

Предельными траекториями в грубых системах могут быть только состояния равновесия и предельные циклы (см. следствие из теоремы 10).

Сформулируем еще следующую теорему, непосредственно вытекающую из необходимых условий грубости.

Теорема 11. У грубой в замкнутой области G системы может существовать только конечное число предельных циклов.

Необходимые условия I-III являются также достаточными для грубости системы вида (А). Именно, имеет место

Теорема 12. Если для системы (А) в области П выполняются условия I-III, то такая система в области G является грубой.

Доказательство теоремы состоит в фактическом построении для всякой измененной системы (А), достаточно близк£Й к системе (А), такого топологического отображения области G в себя, при котором траектории системы (А) отображаются в траектории системы (А) и соответствующие друг другу точки находятся на сколь угодно малом расстоянии друг от друга.

) Отметим, что введение такого пространства весьма естественно не только с чисто математической точки зрения, но и с точки зрения приложений: именно динамические системы, получающиеся из приложений, всегда содержат то или другое число параметров. Каждой совокупности значений параметров соответствует динамическая система, так что пространство параметров рассматриваемой динамической системы можно интерпретировать как пространство динамических систем - частного вида.

Введенное выше пространство динамических систем является очевидно наиболее общим из таких пространств, включающим в себя все «частные пространства».

В заключение сформулируем следующую теорему, которая позволяет охарактеризовать, какое место грубые динамические системы вида (А) занимают среди всевозможных систем, рассматриваемых в замкнутой области G.

Теорема 13. Если система (А) является грубой в области G, то существует бо>0 такое, что все измененные системы {А) , Ьй-близкие к системе (А), также являются грубыми в области G (и имеют ту же качественную структуру).

§ 7. Пространство динамических систем. Всюду плотность грубых (двумерных) динамических систем. При изложении теории грубых систем весьма естественно и удобно ввести пространство динамических систем. Именно, рассмотрим всевозможные динамические системы, правые части которых определены в данной ограниченной замкнутой области G и являются в этой области аналитическими функциями хиу. Введем пространство, точками которого являются такие динамические системы. Расстоянием между двумя точками этого пространства, т. е. между точками, соответствующими динамической системе (Ai):

dx/dt = Pi{x, у), dy/dtQi{x, у) (Ai)

и динамической системе (А2):

dx/dtР2{х, у), dy/dt = Q2{x, у), (Аг)

будем считать максимум модуля выражений

\Plix, У)-Р2{Х, У)\, Шх, y)-Q2{x, У)\, PlX {Х, у) - Р2Х {Х, у) I,

I Р[у {х, у) - Р,у {X, у) 1, I Ql:, {X, У) - Q,x {X, у) I,

\Qiy{x,y)-Q2y{x, у)\.

Будем введенное пространство обозначать через Ra). Очевидно, динамические системы, б-близкие к данной динамической системе (А), соответствующей точке М пространства На, соответствуют точкам На, лежащим на расстоянии, меньшем б от точки М.