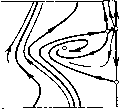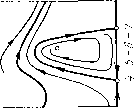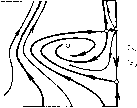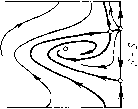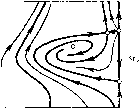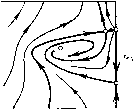о» со

о Рч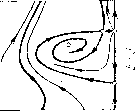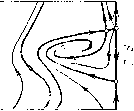

9 = arcsinX~ с возрастанием х точка Pi будет монотонно подниматься, а точки Рз и Pi - монотонно опускаться.

Единственно возможная последовательность бифуркаций ири возрастании р, такая, ири которой слияние точек Pi и Рг предшествует слиянию Pi, Рз и Pi, Ра. Очевидно также, что если последняя из перечисленных бифуркаций осуш;ествляется, то осуш;еств-ляются и остальные. Осутцествимость последней бифуркации следует из того, что при достаточно больших ц (когда максимум изоклины горизонтальных наклонов, равный (Х+1)/х, будет меньше максимума изоклины вертикальных наклонов, равного единице) (о-сепаратриса седла будет иметь всюду отрицательный наклон, и, следовательно, точка Pi будет лежать заведомо выше точки Pi. Очевидно, что в этом случае и предельные циклы, охватываюш;ие фазовый цилиндр, не могут суш;ествовать. Осуществляется структура разбиения фазового цилиндра на траек-торип, представленная на рис. 169,8. Слиянию точек Pi, Рз и Pi, Pi соответствуют расположения сепаратрис, представленные на рис. 169, 5-6 и 169, 6-7. Поведение сепаратрис с точностью до четного числа предельных циклов определяет здесь качественную структуру. Значения параметра р,, соответствующие разбиениям рис. 169,5-6 и рис. 169,6-7, будут бифуркационными. При изменении р, от этих бифуркационных значенш! в направлении возрастания или убывания векторное поле на сепаратрисах поворачивается соответственно по или против часовой стрелки, и сепаратрисы, идущие из седла в седло, разрушаются. Соответствующие грубые структуры изображены на рис. 169,5-169,7.

Заметим, что хотя расположение сепаратрис на рис. 169, 7 и определяет качественную структуру лишь с точностью до четного числа предельных циклов, можно утверждать, что здесь одновременно должны существовать и устойчивый, и неустойчивый предельные циклы, охватывающие цилиндр. Неустойчивый предельный цикл появляется из петли сепаратрисы, охватывающей цилиндр, так как седловая величина сг = Рф -Ь Qp положительна, и ири разрушении петли к ней может стянуться или из нее появиться только неустойчивый предельный цикл (кривая 04 = О представляется уравнением Х(1 - 2х2)= - 3хУ1-Ь р, - Х; она целиком расположена в полосе УЗ/2 <К< 3/2, т. е. вне рассматриваемого пнтервала изменения X).

При дальнейшем увеличении параметра .i векторное поле на каждом из предельных циклов поворачивается ио часовой стрелке; при этом устойчивьш предельный цикл опускается, неустойчивый - поднимается. При любом фиксированном X в рассматриваемом интервале существует единственное бифуркационное значение р*, при котором устойчивый п неустойчивый предельные циклы сливаются, образуя двойной полуустойчивый цикл. Это - последняя бифуркация, возможная при возрастании параметра р,.

) Где симво.ч {к. 1} означает кривую, разделяющую области, обозначенные соответственно чпсла.\1 к и I.

При дальнейшем возрастании р векторное поле па двойном цикле поворачивается по часовой стрелке и двойной предельный цикл исчезает. Негрубая структура разбиенпя иа траектории, соотвег-ствуюпгая значению р = р*, изображена па рпс. 169. 7-8. Д.ля всех р > р* осуш;есгвляется разбиеппе па траекторпи. представленное па рис. 169, S.

4, Таким же образом прослеживаются бифуркации в зависимости от р прн любых фиксированных Я > ТЗ/2. Число возможных бифуркаций здесь уменьшается, по появляются две новые.

1) При убывании р от значений, соответствуюш;их разбиению, представленному на рис. 168, V (для участка граппчпой кривой выше точкп D па рпс. 167), исчезает особая точка седло-узел и из а-сепаратрнсы седло-узла появляется устойчивый предельный цикл (при обратном пзмеиепии р устойчивый предельный цикл превраш;ается в а-сепаратрпсу седло-узла).

2) Так как кривая 04 = О располагается выше прямой Я>"13/2 и образование петли сепаратрисы для некоторых значений Я может осуш;ествпгься прп 04 < О, то для этпх значений h переход от разопеппя типа 169, к типу 169, S ири возрастании р будет происходить путем стягивания устойчивого предельного цикла к петле сепаратрисы, охвагываюш;еп цилпндр. При этом возникает новая пегрубая структура, разделяюш;ая структуры 169,6 и 169,8, представленная па рпс. 169,6-8. Для структуры 169, б-S, как п для структуры 169,6-7, и а- н (о-сепарагрпсы седла Oi образуют петлю, охватываюш;ую цилиндр, по пет устойчивого предельного цикла.

В области И-р2 -Я2<0, рО прп любых "к будут осуш;есгв-ляться структуры 1 п 2 рпс. 169. В области (14-Я)/р<1 - структура 8 рпс. 169. Смепа структур будет происходить при пзмеиепии р в ипгервале между кривой \ + - к - О и прямой 1--Я-р=0 OW\<\x<k+i).

Множество точек, соответсгвуюпгее пегрубым бифуркационным картинам 4-5, 5-6, 6-7 и 6-8 па рпс. 169, образует негрубые кривые {4.5), {5.6), {6.7) и {6.8} *) в плоскости (р, к) (см. рис. 167). Эти кривые пмеют положительный наклон. Последнее следует из того, что при возрастании параметров р п Я в отдельности векторное поле на сепаратрисах, пдуш;пх пз седла в седло и пе пересекаюш;пх контактную кривую (изоклину вертикальных наклонов), поворачивается в противоположных направлениях. Только при одповремеином возрастании плп убывании р и к поворот векторного поля вдоль сепаратрис, пдупгих из седла в седло, может быгь пе монотонным и пе разрушаюпгпм сепаратрисы.