
 |
|
Главная страница Приемы качественного исследования [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [ 140 ] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] вое из равенств (5) неявно определяет функцию 9 = 9(р)-время перехода из фиксированного и на полупрямую U\. Ее предельное значение при р О (доказательство аналогично доказательству в приложении I) есть 9 = rln[rp/(rp-tt)]. (8) Во втором из равенств (5) положим 9 = 9(р) и найдем lim Ml [9(р), р] при р 0. Это предельное значение есть И1 = 0. (9) Фиксируем теперь и = г. Рассмотрим изменение отрезка "о"Ео(р) с уменьшением р. Для этого вычислим Uo(0)=-2P(4/i>b+l)/[r(P-7)]. Если Ь > - 1/(4fe), то при малых р величина uo убывает вместе ори точка и = г участвует в преобразовании S. Первое из равенств (5) определяет функцию 9 = 9(р) -время перехода из и = гр на полупрямую Ui. Ее предельное значение при р->-О есть 9 = 0° (это следует из того, что 9 в равенстве (8) можно сделать как угодно большим, если взять и достаточно близким к г, и из того, что в S производная ди1дд>0). Случай Ь < - 1/ (4fe) рассматривается аналогично. Величина Ио возрастает с уменьшением р, и точка и = г участвует в преобразовании Т. Предельное время есть т=0°. При Ь=»-l/(4/i) имеем ио. В этом случае точка и=Г при любом р лежит на сепаратрисе. Время доопределенного движения есть оо. Для и<г{ - ) нужно егце получить уравнения движения изображающей точки по прямой ф = фо. Для любого и это будет y-Y{t)0. (10) Полученная схема доопределяемых движений по верхней части прямой ф = фо приведена на рис. 219, а. Здесь для наглядности налегающие одна на другую траектории раздвинуты в горизонтальном направлении. Изображающая точка системы (2), попавшая в точку (ф = фо, у = и), и г(Р - ), совершает мгновенный скачок в соответствии с формулой (7) и продолжает движение при ф>фо в соответствии с системой (2). Если < и < г(р - Y), то изображающая точка перескакивает в точку г; = О, находится здесь в течение времени (6) и затем двигается при ф > фо. При и = г изображающая точка перескакивает в точку (ф = фо, = 0) и остается там неограниченно долго. Это движение является вырождением при р. О движения по сепаратрисе седла системы (3). Если и < г, то изображающая точка мгновенно перескакивает в точку ui = О и находится здесь в течение времени, опреде- ляемого формулой (8), после чего продолжает движение при Ф < фо. Из соображений симметрии следует, что если в описанной схеме поменять и на fi, у на щ, р на -f и наоборот, то получим схему доопределенных движений по нижней части прямой ф = фо- 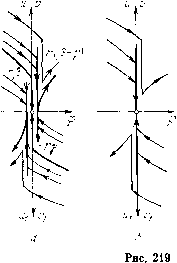 II. р < о < "I, г 1ЪЬ, < 0. Состояние равновесия системы (3) при малых р, - устойчивый узел, лежащий в полосе -р, < ж < р.. Соответствующая картина фазовых траекторий приведена на рис. 218, б. Пусть Uo = uo(n)-отрезок, отсекаемый на полупрямой U траекторией, проходящей через точку (х = р., у = 0). При р, О имеем wo(tt)- г(р - f), "о(л)->-+ оо- Поэтому для «>r(p-f) вычисления совпадают с соответствующими вычислениями п. 1. Если же полутраектория системы (3) начинается на отрезке U гр(р - f), то при малых р, она целиком лежит внутри полосы -[X < X < р., и время соответствующих доопределенных движений есть CXD. Уравнением движения по прямой ф = фо, как и в случае I, будет уравнение (10). Полученная схема доопределяемых движений по верхней части прямой ф = фо приведена на рис. 219, б. Изображающая точка системы (2), попавшая в точку (ф = фо, у = и), u>r(p -f), совершает мгновенный скачок в соответствии с формулой (7) и продолжает движение прп ф > фо в соответствии с системой (2). При и < г(Р - y) изображающая точка мгновенно перескакивает в точку (ф = фо, У = 0) и остается там неограниченно дол- ГО. Будем говорить, что эти движения ведут в состояние равновесия (ф = фо, г/ = 0), являюш;ееся вырождением при р->-О узла системы (3). Из соображений симметрии следует, что если в описанной схеме поменять и на v\, v на и\, то получим схему доопределенных движений по нижней части прямой ф = фо. III. О <f < р, r=2&/i>0. Состояние равновесия системы (3) есть седло, расположенное правее полосы -р <x<\i. Не приводя вычислений, опишем получающуюся в этом случае схему доопределеипых движений (рис. 219, в). Изображающая точка спстомы (2), попавшая в точку (ф = фо, у = и), и> >r(fi -), совершает мгиовеиный скачок в соответствии с формулой (7) и продолжает движение при ф > фо в соответствии с системой (2). Если iisSr(p -y), to изображающая точка мгновенно перескакивает в точку lii = О и находится здесь в течение времени, определяемого формулой (8), после чего продолжает движение при ф < фо. Изображающая точка системы (2), попавшая в точку (ф = фо, у = v\), v\ > г(р - f), совершает мгновенный скачок вверх в соответствии с равенством u\ = v\ - г(р - "у) и продолжает движение при ф < фо в соответствии с системой (2). Если vi < <г(р -), то изображающая точка мгновенно перескакивает в точку Ц] = О и остается здесь в течение времени т = г X X\n[rfl{г\ +v\)], после чего продолжает движение при ф < фо. IV. О < р < г 2bh < 0. Состояние равновесия системы (3) при малых р - устойчивый узел, лежащий левее полосы -[i <х< \i. Схема доопределенных движений та же, что и в п. III. Случай V: р<<0, г<0, и случай VI: <Р<0, г>0, получаются соответственно из случаев IV и III заменами: на -i, и на f 1, у па Ml и наоборот. Из имеющихся шести случаев получим еще шесть, соответствующих изменению знака г, заменами: р на -f, г на -г, и на V, и\ на v\ и наоборот. Рассматривая точечные преобразования прямых ф = фо самих в себя, осуществляемые доопределенными движениями, совместно с точечными преобразованиями прямых ф = фо самих в себя и одной в другую, осуществляемыми траекториями системы (2), можно провести качественное исследование системы для конкретной характеристики Р(ф), имеющей разрывы. Пример 1. Пусть Р(ф)-функция периода 2я такая, что F (ф) = ф/я при -я < ф < я, и пусть О < < 1. Этот пример иллюстрирует первый случай доопределения. В качество фазового пространства будем рассматривать полосу, заключенную между прямыми ф = -я и ф = я. Точки этих прямых, имеющие одинаковые ординаты, отождествляем. Таким образом, точки разрыва характеристики находятся на линии склейки цилиндрического фазового пространства. [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [ 140 ] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] 0.0111 |