ГЛАВА 2

ВОЗМОЖНЫЙ ХАРАКТЕР ОТДЕЛЬНОЙ ТРАЕКТОРИИ. ТЕОРИЯ ПУАНКАРЕ - БЕНДИКСОНА. ОСОБЫЕ ТРАЕКТОРИИ

Введение. В настоящей главе приведены те определения и предложения, на основании которых устанавливаются свойства траекторий системы

х = Р{х, у), y = Q{x, у) (А)

и свойства разбиения на траектории, являющиеся основными в вопросах качественного исследования. На основании этих предложений:

1) сформулировано, каков возможный характер отдельной траектории системы (а);

2) выделены некоторые особые траектории, знание взаимного расположения которых необходимо для определения качественной структуры разбиения на траектории;

3) дано понятие схемы динамической системы).

Все предложения настоящей главы, позволяющие сделать весьма далеко идущие заключения относительно возможных свойств разбиения на траектории, заданного системой (а), фактически являются следствием двух основных общих теорем - теоремы о существовании и единственности решения и теоремы о непрерывной зависимости от начальных значений, но при этом существенно опираются на тот основной элементарный факт, что простая замкнутая кривая делит плоскость на две области.

Во всех этих предложениях в качестве вспомогательного средства используется дуга без контакта и цикл без контакта.

§ 1. Дуга без контакта. Пусть i - простая г.ладкая дуга), целиком лежащая в области g, в которой определена система (А).

) Подробные доказательства всех приведенных в настоящей главе утверждений, касающихся характера отдельной траектории (см. [12, 76, 134]). Об особых траекториях см. в [12, 81], а также в [63, 64, 154].

2) Простой гладкой дугой называется дуга, которая может быть задана параметрическими уравнениями х = f{s), у = g{s), удовлетворяющими следующим условиям.

Функции /(s) и g{s) определены на некотором сегменте (отрезке) значений S, Sl S S2, И при ЭТИХ значениях непрерывны и имеют непрерыв-

Если траектория системы (А), проходящая через точку М дуги Z, в этой точке не касается дуги Z, то мы будем говорить, что дуга I в точке М не имеет контакта с траекториями системы (А). Если же проходящая через точку М траектория касается дуги, то мы будем говорить, что дуга I в точке М имеет контакт С траекторией системы (А). Простая гладкая дуга называется дугой без контакта для траекторий системы (А), если:

а) на I не лежит ни одно состояние равновесия;

б) ни в одной своей точке дуга I не имеет контакта с траекториями (рис. 18).

Мы скажем, что дуга I проведена через точку М (или в точке М), если точка М является точкой дуги без контакта I, отличной от концов этой дуги. Очевидно, через каждую неособую точку можно провести дугу без контакта (например, достаточно малый отрезок нормали к траектории будет отрезком без контакта - дугой без контакта).

Пусть параметрическое уравнение дуги без контакта I есть x = f{s), y = g{s), где /(s) и g{s)- непрерывные функции, определенные при всех значениях

а < S 6

и в силу требования гладкости дуги имеющие при этих значениях непрерывные производные /(s) и g{s). В силу условия а) при всех s, а < s < 6,

РЧН), g{s))+Q4f{s), g{s))¥0.

В силу условия б) при всех s, а < s < 6,

P{f{s),g{s)) /()

Q{f{s),g{>)) g{s)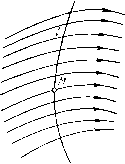

Рис. 18

А(.) =

В случае, когда дуга I задана не параметрическими уравнениями, а уравнением

F{x,y) = Q, (2)

мы будем, очевидно, иметь в силу условия а) ири всех значениях X, у, удовлетворяющих уравнению (2),

РЦх, y)+QHx, У)Ф0

ные производные. Ни при каких двух различных значениях s и s", si s S2, S, s" $2, Нв могут одноврвмвнно ВЫПОЛНЯТЬСЯ равенствя /(s) =/(s"), g{s) = g{s"). (Простая дуга есть гомеоморф (см. § 14 гл. 1) сегмента (отрезка).)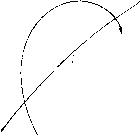

3) Точное определение сторон дуги (см. [12], Приложение).

*) Простой замкнутой привой навывается кривая, которая является топологическим образом окружности. Она является гладкой, если в каждой ее точке существует касательная.

И В силу условия б) при тех же значениях х ш у

fI (х, у) Р {х, у) + Fy {х, у) Q {х, у) Ф 0. (3)

Так как угол между дугой без контакта I и любой пересекающей ее траекторией не обращается в нуль, то, очевидно, этот угол сохраняет постоянный знак.

Если данную гладкую дугу I пересекает другая гладкая дуга ll в точке Мо, отличной от концов Z (касательные к дугам I ш li в точке Мо различны), то точка Мо делит дугу U на две части,

из которых одна лежит по одну сторону i, а другая по другую сторону Р).

Приведем два элементарных предложения, касающихся иересечения траектории с дугой без контакта:

I. Если аир (а < Р)- произвольные числа из интервала (т, Т), на котором определено соответствующее траектории L рещение, то часть траектории L, соответствующая значениям пз сегмента а < i может иметь лищь конечное чис-Рис. 19 ло общих точек с любым отрезком без

контакта.

II. Если Мо - очка дуги I, отличная от ее концов, то всякая траектория, при t - to проходящая через точку М в достаточно малой окрестности точки Мо, непременно пересекает дугу I и при этом при значении Т, сколь угодно близком к to (если точка М достаточно близка к Мо). Если траектория пересекает какую-нибудь дугу I без контакта дважды, то она, очевидно, может пересечь ее только так, как показано на рис. 21 (и невозможен случай, представленный на рис. 19).

§ 2. Цикл без контакта. Пусть С - гладкая простая замкнутая кривая), лежащая в области G. Мы будем говорить (так же, как и в случае простой дуги), что кривая С в некоторой своей точке М не имеет контакта, если проходящая через точку М траектория системы (А) не касается кривой С в этой точке, и будем говорить, что кривая С в точке М имеет контакт, если проходящая через точку М траектория в этой точке касается кривой С.

Гладкая простая замкнутая кривая С называется циклом без контакта, если: а) на С не лежит ни одно состояние равновесия системы; б) ни в одной своей точке кривая С не имеет контакта (рис. 20).