узел. При значениях % ш d, взятых из области 2, происходит появление устойчивого предельного цикла из а-сепаратрисы седло-узла.

При Y = О фазовое пространство симметрично относительно начала координат (рис. 183). Состояния равновесия будут Oi(0,0)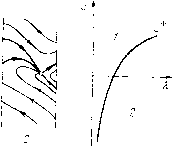

Fkc. 181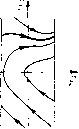

и 2(0, ±п). Если существует петля сепаратрисы на верхнем полуцилиндре, то существует и петля снизу. Такая двойная петля образует также замкнутый контур вокруг состояния равновесия Ои Это значит, что кривые L~, L° и совпадают. При y О кривые L- и L+ сближаются и сливаются при y = О с осью d и /у°-кривой. Точки /у++-кривой при убывании y становятся внутренними точками области 6 (см. рис. 180). Область 7 не может сохраниться при Y = О, так как это означало бы, что и при достаточно малых y будет существовать четыре цикла. При y О кривая влипает в полупрямую Х = 0, d<-i. При y = 0 на плоскости параметров (К, d) будет единственная бифуркационная L-кривая, возникающая из слияния кривых L~, и Кривая L начинается в точке (К = О, d = 3) и уходит в бесконечность. Она не может пересечь ни прямую d = 1 (так как P<f + Qv = - (1 - dcos ф) не меняет знак при \d\ 1), ни прямую Я = О (так как с А;-кривыми не может быть более одной точки пересечения). При переходе через L-кривую вдоль А;-кри-вых прп возрастании X и возникновении двойной петли к каждой полупетле стягивается устойчивый предельный цикл (так как седловая величина {Pq, + Qy} = - X{i + d) отрицательна, a векторное поле поворачивается по часовой стрелке). При дальнейшем изменении К и разрушении петли от двойной петли, рассматриваемой как замкнутый контур, охватывающий состояние равновеспя 0\, появляется устойчивый предельный цпкл, охватывающий это состояние равновесия. Предельный цикл стягива-23*

Рис. 182

ется в точку при d = l, и фокус становится устойчивым. Пространство параметров и структуры разбиения фазового пространства ДЛЯ Y = О изображены на рис. 183.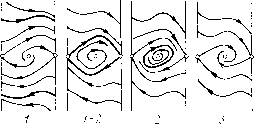

с/=1

Рис. 183

Приложение I. Для исследования поведения траекторий при больших > О полагаем у = 1/р. Система (1) переходит в систему

1 dp „

или в уравнение

dp о в

= р (А, - А; cos ф) + р" (sin ф - у),

где риф можно рассматривать как обычные полярные координаты на плоскости, перпендикулярной оси фазового цилиндра. Преобразование у = 1/р переводит спирали, охватывающие цилиндр, в спирали, охватывающие состояние равновесия в точке р = 0. Решение уравнения (А), определяемое начальныл! условием р = ро > О при ф = О, можно искать в виде ряда

Р = Po"i (Ф) + Ро"2 CP) + Ро"з (Ч») + Ро"4 (Ф) + • •

сходящегося для всех ф в интервале -п ф п и для всех достаточно малых значений ро. Последовательно определяя обычным путем из рекуррентных уравнений функции И1(ф) = 1, "2(ф), ... и полагая затем ф = 2я, получаем на отрезке ф = О функцию последования. Уравнение

Pi - Ро = Ро"2 (2) + Ро"з (2) + Ро"4 (2") + .. •

= р1 [2пХ + [(2яА,) - 2яу] р + [(Inlf - 2пА, (5яу + D - М Р + •.. 1 = О

при Y = О и малых Я, (для любого > 0) имеет положительный корень, соответствующш"! устойчивому предельному циклу на верхнем фазовом полуцилиндре. При "f = О в силу симметрии траекторий фазового пространства (полосы -п ф п) относительно начала координат будет существовать и симметрично расположенный устойчивый предельный цикл на нижнем полуцилиндре. Оба предельных цикла сохранятся и при малых

При малых Y и А, и любых к>-пу будет осуществляться структура разбиения фазового цилиндра, представленная на рис. 183, 1.

Приложение II. Уравнение (В) в приложении I будет иметь при малых "f и малых ро == ijy двойной положительный корень, соответствующий двойному предельному циклу на верхнем фазовом полуцилиндре, если

А, =-f/(2А;)-I-..., т=0, А,#0, k<Q.

ЧАСТЬ IV КУСОЧНО-СШИТЫЕ СИСТЕМЫ

ГЛАВА 17 ОБЩИЕ СВЕДЕНИЯ О КУСОЧНО-СШИТЫХ СИСТЕМАХ

Введение. В последующих главах настоящей книги рассматриваются так называемые «сшитые» и «склеенные» динамические системы.

Так называются системы, область определения которых G (могущая совпадать со всей плоскостью (х, у)) разделяется на подобласти Gi, в которых определены различные аналитические системы. Траектории этих частичных систем сшиваются тем или другим образом (в зависимости от задачи) на границах Gi.

К рассмотрению таких сшитых динамических систем естественно приводят многие задачи из приложений, например, осциллятор с сухим трением, системы с «ударами» (простейшие модели часов), простейшие задачи регулирования (двухпозиционный авторулевой) и др. (см. [2, 3]).

Такие системы имеют некоторые типичные черты, именно:

1. «Сшитость» системы (а также «условия сшивания») непосредственно вытекает из физического смысла рассматриваемой задачи.

2. Система является кусочно-линейной, т. е. те частичные системы, из которых она склеивается, являются линейными.

3. На линии склейки может быть определено точечное отображение (функция последования), которое позволяет определить характер рассматриваемой системы.

В частности, в [3] приведено большое число примеров таких систем и дано рассмотрение их методом точечных отображений. При этом в большинстве из этих задач точечное отображение рассматривается записанным в параметрической форме, т. е. не в виде y = f{y), а в виде = /i(p), y==f2{p), где р - параметр. Такая параметрическая форма в некоторых случаях существенно упрощает рассмотрение. Во многих случаях полученное упрощение, приводящее к рассмотрению сшитой системы, позволяет рассматривать значительно более сложные фазовые пространства, чем плоскость. Однако в настоящей книге такие задачи не рассматриваются.

В случае, когда сшитая система хорошо отображает черты реальной системы, рассмотрение ее методом точечных отображений позволяет, вообще говоря, не только устанавливать качест-