лишь различное расположение на плоскости параметров бифуркационных кривых на интервале О < Y < 1 (рис. 240). Уравнению (1) эквивалентна система

dcp/dt = yP, dy/dt =- hy -F((f)Q (3)

илп уравненпе

dy y - hy - F((f) d(p у

Будем рассматривать (3) и (4) на фазовом цилиндре -я = < Ф я (прямые ф = ±я отождествляются). Два состояния равновесия (3) или две особые точки (4) располагаются на оси у = = 0 и для любых характеристик класса F{(f) будут фокус и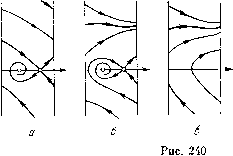

седло. Характер состояний равновесия определяется по корням характеристического уравнения и будет зависеть от знака Р(ф) в соответствующей точке. Производная Р(ф) в двух соседних особых точках имеет разные знаки. Для h> О фокус устойчивый. При Y = 1 особые точки сливаются, образуя особую точку типа седло-узел.

Критерий Дюлака (см. гл. 6) позволяет сделать исчерпывающие высказывания о бифуркациях, связанных с предельными циклами. Так как величина Pq, + Qy= - h не меняет знака в рассматриваемой области пространства параметров, то не существует предельных циклов, ох1ватывающих состояние равновесия, и не может быть более одного предельного цикла, охватывающего фазовый цилиндр. Бифуркации, связанные с появлением предельного цикла из сгущения траекторий (связанные с рождением двойного предельного цикла), для рассматриваемого класса характеристик невозможны.

Условие (2) позволяет утверждать, что бифуркация, связанная с петлей сепаратрисы, возможна только в верхнем полуцилиндре {у>0). В самом деле, если существует замкнутый контур, составленный из интегральных кривых уравнения (4), то

должно быть

[У-%(Ф)-(Ф)]ЙФ4- \ dly{cp)f = 0

ИЛП в силу (2)

но это невозможно при г/(ф)< О и положительных й и у. Каждая траектория системы (3) на нижнем полуцилиндре пересекает ось у == О (если только она не будет м-сепаратрисой седла).

Теперь остается установить для характеристик рассматриваемого класса возможность бифуркаций, связанных с появлением предельного цикла из петли сепаратрисы в верхнем полуцилиндре.

Для определенности выберем так начало отсчета по координате ф, чтобы для характеристики F{(p) выполнялись условия F(-л)=0, F(-я)<0 (для системы (3) это всегда возможно)]. Другой корень уравнения /(ф)= О обозначим фо.

Введем систему сравнения (5)

Ф(Ф) =

1, - Я<ф<фо, О, Фо<Ф<я.

Характеристика Ф(ф) расположена ниже характеристики (ф) системы (3). Векторное поле системы (5) повернуто по отношению к векторному полю системы (3) на положительный угол на верхнем полуцилиндре.

Качественная структура разбиения фазового пространства и пространства параметров системы сравнения (5) могут быть легко получены. Для системы (5) при й > О и y > О суп1;ествует лишь одна структура разбиения фазового пространства на траектории. Все траектории идут из бесконечности к устойчивому предельному циклу на верхнем полуцилиндре, расположенному в полосе (y + 1)/й < Ф < iJh.

Проследим поведение траекторий системы (3) на верхнем полуцилиндре, используя сведения о поведении траекторий системы (3) при й = 0 и систему сравнения (5).

Рассмотрим разбиение на траектории для системы (3) при й = 0 (0<y<1). Уравнение (4) интегрируется. На фазовом цилиндре две особые точки: (у = О, ф =ф1) (центр) и (у = О, ф = ф2) (седло); фь ф2-корни уравнения y -(ф) = 0 (ф2>

J 4] ИССЛЕДОВАНИЕ РОЛИ АППРОКСИМАЦИЙ 447

>9i). Уравнение сепаратрис, проходящих через седло, будет

г/2 = 2у(ф-ф,)-2Ф(ф), Ф(ф) = j (ф)йф. (6)

Функция Ф(ф)- периодическая с периодом 2л, кусочно-монотонная с двумя экстремумами на периоде в точках ф = -л (ф = л) и Ф = фо, обращающаяся в нуль в точках фг и ф2( - л < Фа < Фа).

Уравнение

Т(ф-Ф2)-Ф(ф)=0,

кроме двойного корня ф = фг, всегда имеет ири О (О < < < 1) единственный простой корень ф= ф* (- л <; щг <; Ф* <: фг). Поэтому сепаратриса (6) при О < f < 1 образует петлю, охватывающую состояние равновесия ф = ф1. Отметим, что а-сепаратриса седла иа верхнем полуцилиндре пе может возвратиться в то же седло и, накручиваясь на цилиндр, уходит в бесконечность (ири h = О бесконечность устойчива).

Лишь при y = О будет ф* = ф2 = - л и сепаратриса образует петлю, охватывающую цилиндр. Для любого ФО (О < <-<1) всегда можно выбрать столь малое h, что а-сепаратриса седла на верхнем полуцилиндре также будет накручиваться на цилиндр. Так как при h> О бесконечность для системы (3) неустойчива, то отсюда следует существование для малых h устойчивого предельного цикла, охватывающего цилиндр (единственного в силу критерия Дюлака) (рис. 240, б).

Для больших h структуру разбиения фазового пространства на траектории можно установить, используя систему сравнения (5). Па верхнем полуцилиндре изображающая точка, двигающаяся по траектории системы (3), слева направо пересекает траектории системы (5) сверху вниз. Пусть у -= ц есть точка пересечения со-сепаратрисы седла на верхнем полуцилиндре с прямой ф = фь Если выбрать h так, чтобы верхний край полосы, содержащий предельный цикл системы (3), лежал ниже прямой у = т] и, следовательно, выполнялось условие {+l)/h<r\, то ю-сепаратриса седла на верхнем полуцилиндре попадет в область (выше полосы, содержащей предельный цикл системы (5)), заполненную траекториями, пересекающими траектории системы (5) сверху вниз. В этом случае предельный цикл системы (3) не может существовать. Такой выбор h при О < y < 1 всегда возможен, так как с возрастанием h векторное поле поворачивается по часовой стрелке и, следовательно, Т1 растет (рис. 240, а).

Из сравнения структур разбиения фазового пространства для малых и для больших h следует существование при О < < Y < 1 бифуркационной кривой, для точек которой а- и со-се-