дения о том, каков возможный характер замкнутых траекторий. Эти сведения имеют также первостепенный интерес для понимания поведения предельных циклов при изменении параметра. Пусть Lo - замкнутая траектория,

- какое-нибудь соответствуюгцее ей движение, являющееся периодическим с периодом т. Если I - дуга без контакта, проведенная через какую-нибудь точку Q траектории Lo, то на части этой дуги, достаточно близкой к точке Q, будет определена функция последования (см. § 1 настоящей главы). Пусть s - параметр на дуге I, so - значение этого параметра, соответствующее замкнутой траектории Lo, и s =/(s)-функция последования. Введем функцию

yjp{s) = f{s)~s.

Очевидно,

i)(so) = 0.

Разложим yJp (s) в ряд по степеням s - sq:

i)(s) = ai(s-so)-f a2(s-so)2 + ..., a, = /(so)~l, a, = f{so)li\.

Возможны следующие случаи).

1. /(so)=l.

Корень so функции ij5(s) очевидно изолированный, замкнутая траектория является простым предельным циклом - устойчивым, когда

/(so)< 1, т. е. t)(so)<0, и неустойчивым, когда

/(so)>l, т. е. i;(so)>0.

2. /(so)=l, т. е. tN) = 0,

но хотя бы одна из производных функции (s) не обращается в нуль при s = so, т. е. существует такое к, что

(so) = ... = t"" (so) = О, kla = (so) Ф 0.

Мы будем иметь, следовательно,

ij5(s) = (s-so)[afc-f aft+i(s-so)+ ...].

Корень so функции iJ5(so), так же как и в случае 1, изолированный. Замкнутая траектория Lo называется сложным к-кратным предельным циклом.

) Проведенное здесь рассмотрение во многом аналогично проведенному в § 5 гл. 3.

а) к нечетное. Предположим, что ij;* (о) = < 0. Тогда при S < So

а при S > So

t{s)>0, т. е. f{s)>s, Ti:(s)<0, т. е. f{s)<s.

Следовательно, всякая последующая точка на отрезке I ближе к точке Q (в которой замкнутая полутраектория Lq пересекает отрезок I), чем предыдущая. Так как по самому построению функции последования последующая точка соответствует значению t большему, чем предыдущая, то, принимая во внимание, что Lo - единственная замкнутая траектория, пересекающая рассматриваемую часть отрезка без контакта I, нетрудно показать, что всякая отличная от Lq траектория, пересекающая отрезок I достаточно близко к точке Q, при t +«> стремится к предельному циклу Lq. Предельный цикл Lo является устойчивым (нечетно-кратным) предельным циклом (рис. 64, а).

Если ф* (so) > О, то совершенно так же можно показать, что всякая траектория, пересекающая отрезок I достаточно близко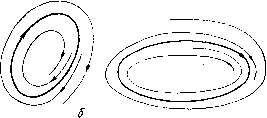

Рис. 64

Рис. 65

к точке Q, при t -°о стремится к предельному циклу Lq. Предельный цикл Lo является неустойчивым (нечетно-кратным) предельным циклом (рис. 64, б).

б) к четное. Тогда при s¥=so в зависимости от знака а* = г1>Ч«о) либо t(s)>0, т. е. f{s)>s (если t*** («о)>0), либо i)(s)<0, т. е. /(s)<s (если ф*Чо)< 0). Нетрудно показать, что в случае, когда г])*** (so) > О, все траектории, проходящие через точки отрезка I, соответствующие значениям s < Sq, стремятся к Lo при t -Ь<», а все траектории, проходящие через точки отрезка I, соответствующие значениям s > so, стремятся к Lo при t-v-оо, и наоборот, когда iJ5>(so)<0 (рис. 65).

Очевидно, в рассматриваемом случае (четное к) предельный цикл Lo неустойчив. Однако часто предельный цикл этого типа

называют полуустойчивым {четно-кратным), сохраняя термин «неустойчивый» лишь для цикла, к которому все достаточно близкие траектории стремятся при t -°о.

3. Производные всех порядков от функции Ир {s) при s = so равны нулю, т. е. при всех i (so) = 0. Тогда 1р(5) = 0, т. е.

функция послед9вания имеет вид

В этом случае все траектории, проходяп1;ие через достаточно близкие к Lo точки, замкнуты (этот случай аналогичен случаю центра).

На рис. 61 и 62 даны диаграммы Ламерея для случая нечетно-кратного предельного цикла (см. рис. 62) и четно-кратного предельного цикла (см. рис. 61).

Рассмотрение функции последования, в частности условий кратности замкнутой траектории, было проведено при определенном выборе дуги без контакта. Однако шожно показать, что эти условия не зави-/сят от выбора дуги без контакта и от выбора параметра на этой дуге (при условии, конечно, что параметрические уравнения рассматриваемых дуг являются аналитическими функциями).

Далее, из ироведенного исследования функции последования, в котором суп1;ественно использовался тот факт, что функция последования является аналитической функцией, очевидно вытекает, что у системы с аналитическими правыми частями:

1) не может существовать бесчисленное множество предельных циклов, накапливающихся к замкнутой траектории;

2) не может существовать замкнутая траектория такая, что вне (внутри) нее все траектории не замкнуты, а внутри (вне) нее - замкнуты, т. е. не может осуществляться, например, случай, представленный на рис. 66.

Указанные свойства могут быть сформулированы в виде следующего предложения.

Теорема 1. Если у динамической системы (А), правые части которой - аналитические функции, существует замкнутая траектория, то она либо является изолированной, либо все траектории в ее окрестности замкнуты.

Ряс. 66

Рис. 67