dy у dx X

+ с.ху- + с,х-у -f ... -f ху F {X, у)

где с, - величины, имеющие тесные связи с ляпуновскими величинами.

В настоящее время рассматривается приведение к нормальной форме не обязательно аналитических систем и аналитическими преобразованиями, а вообще гладких до некоторого порядка систем гладкими же преобразованиями. При этом каноническая форма Дюлака в случае рационального X существенно упрощается.

Отметим, что нормальной формой в случае одного нулевого корня (см. § 3 гл. 4) является

ах -f сх

(но с может обращаться в нуль).

В настоящей книге нормальные формы в явном виде не используются.

§ 4. Нормальные формы. В последнее, время широкое распространение получило рассмотрение так называемых «нормальных форм» дифференциального уравнения в окрестности особой точки (состояния равновесия). «Нормальная форма»-это максимально простой вид дифференциального уравнения в окрестности особой точки после надлежащим образом подобранной замены переменных, в котором: во-первых, важные для характеристики особой точки величины оказываются выписанными в явном виде (например, ляпуновские величины) и, во-вторых, в некоторых случаях уравнение в окрестности особой точки приводится к интегрируемому виду. Если существует преобразование переменных, при котором система делается линейной, то ее нормальная форма - линейная. Дюлаком были рассмотрены те нормальные формы, к которым могут быть приведены дифференциальные уравнения (с аналитическими правыми частями) в окрестности седла.

В зависимости от того, является ли модуль отношения характеристических чисел седла Xi и 2, т. е. \X\IX2\ = X, рациональным или иррациональным, эти формы различны. Именно, Дюлак показал, что когда к иррационально, аналитической заменой переменных можно привести дифференциальное уравнение к виду

где I ж к - любые целые числа. Однако привести такое уравнение, несмотря на то, что I ж к могут быть сколь угодно большими, к линейному виду может оказаться невозможным, так как преобразование, приводящее к линейному виду, окажется расходящимся рядом.

Когда к рационально {К = mjn), Дюлак приводит уравнение к виду

ГЛАВА 5

ФУНКЦИЯ ПОСЛЕДОВАНИЯ. ПРОСТЫЕ И СЛОЖНЫЕ ПРЕДЕЛЬНЫЕ ЦИКЛЫ

§ 1. Функция последования. В настоящем параграфе рассматривается функция последования, которая уже использовалась при исследовании состояния равновесия, у которого А > О, а>0. В настоящей главе функция последования используется для исследования окрестности замкнутой траектории.

Пусть I - дуга без контакта, и пусть на этой дуге введен параметр s так, что каждой точке I соответствует взаимно однозначно одно значение s, si s S2, si и s2 - некоторые фиксированные значения.

Пусть

x = l{s), y = m{s)

- параметрические уравнения дугп I, которые даются с помощью введенного параметра s. В дальнейшем мы всегда будем предполагать, что в рассматриваемом нами случае, когда правые части системы (А)-аналитические функции, функции l{s) и m{s) также аналитические функции

Предположим, что траектория L, пересекающая при t = to дугу I в точке Q, соответствующей некоторому значению s, пересекает дугу I еще раз при некотором значении t > to. Пусть ii - первое значение, большее to, при котором L пересекает дугу I, Q - соответствующая точка и я - значение параметра s в этой точке (рис. 59).

Мы скажем, что точка Q дуги I имеет последующую Q. Если обе точки Q к Q отличны от концов дуги I, то на основании теоремы о непрерывной зависимости от начальных условий и предложения II § 1. гл. 2 у всех точек дуги I, близких к Q, будут существовать, последующие (в частности, это всегда имеет место, когда траектория, проходящая через точку Q, замкнута).

Пусть s и я - координаты различных точек дуги I и их последующих на отрезке s. Ясно, что s является функцией от s. Эта функция

s=f{s)

) В случае, когда дуга I не является аналитической дугой, всегда можно приблизить ее аналитической дугой так, чтобы эта новая аналитическая дуга также являлась дугой без контакта.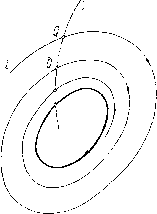

Рис. 59

называется функцией последования и выражает собой закон некоторого точечного преобразования дуги I (или ее части), устанавливающий однозначное соответствие между точками этой дуги (или ее части) и их последующими (на той же дуге I).

Геометрически ясно, что функцию последования мы имеем тогда, когда дугу 6ie3 контакта пересекают траектории, имеющие характер спиралей или замкнутые (см. рис.59). При этом очевидно, что если некоторому значению S = So соответствует замкнутая траектория, то /(so) = so, т. е. точка, соответствующая S = So, и ее последующая совпадают (а значит, совпадают и все дальнейщие последующие). Очевидно и обратное: если /(so)=so, то траектория, проходящая через точку, соответствующую значению so, замкнута. Точка, для которой /(so)=so, называется неподвижной или инвариантной, точкой точечного отображения.

Для функции последования справедливо следующее:

1. Функция последования для аналитической системы (А) при сделанном предположении относительно аналитичности дуги без контакта (функции l(s) и m(s) в параметрических уравнениях дуги - аналитические функции) является аналитической функцией. (Это предложение является следствием теоремы 3 гл. 1.)

2. Производная от функции последования всегда положительна (т. е. функция последования - всегда возрастающая функция). Это предложение фактически является элементарным следствием того факта, что траектории не пересекаются.

Введение функции последования позволяет для формулировки вопросов устойчивости и неустойчивости замкнутой траектории использовать вопросы устойчивости и неустойчивости неподвижной точки точечного отображения s = f(s).

Пусть рассматриваемой замкнутой траектории Lq соответствует неподвижная точка s* точечного отображения s =/(s). Рассмотрим последовательные точки пересечения с дугой I какой-нибудь траектории L, отличной от Lq и проходящей через достаточно близкую к Lq точку.

Пусть траектория L пересекает отрезок в точках, соответствующих значениям s

При этом

S2=/(Sl), S3 = /(S2), S„+1=/(S„).