
 |
|
Главная страница Приемы качественного исследования [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [ 100 ] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] структура рис. 159,5 с двумя предельными циклами, между которыми нет состояний равновесия. На интервале 1<Я<Л" при некотором X = Я" предельные циклы сливаются в двойной полуустойчивый предельный цикл (рис. 159,4) и затем исчезают. Последовательность структур вдоль нижней ветви дискриминантной кривой представлена на рис. 159,i-10. 3.5. Структуры разбиения фазового пространства и бифуркации внутри дискриминантной кривой в области трех состояний равновесия. Дискриминантная кривая, представленная в параметрическом виде уравнениями (3), может рассматриваться как огибающая семейства прямых а - Ххо - ф(а:о)= О в плоскости {X, о). Полупрямые а-Ххо-{х<}) = 0, Х<-(р{хо), (16) касающиеся в точке Я = - ф(а;о) дискриминантной кривой, однократно покрывают область, ограниченную линией симметричных структур и нижней ветвью дискриминантной кривой, при хо, изменяющемся от точки перегиба до минимума характеристики ф() (при & < Зааго < & + - Зас). Движение в пространстве параметров X, о вдоль полупрямых (16) от точки касания соответствует для системы (1) повороту против часовой стрелки изоклины а - Хх - у = 0 вокруг седла, возникшего в точке х = хо прп разделении седло-узла па седло и узел. Рассмотрим бифуркации, осуществляющиеся при движении по полупрямым (16), касающимся дискримпнантной кривой на интервале Xi<X<Х2. Здесь возникнут как бифуркации состояний равновесия, так и бифуркации сепаратрис и предельных циклов. При уменьшении X состояние равновесия седло-узел внутри устойчивого предельного цикла разделяется на седло и неустойчивый узел, который при дальнейшем уменьшении X превращается в фокус (рис. 160, ii). В точках пересечения рассматриваемой полупрямой (16) с прямыми Li = 0 и L2 = О происходят бифуркации состояний равновесия: при уменьшении X сначала из фокуса xi (рис. 160, iO) и затем из фокуса Х2 рождаются неустойчивые предельные циклы (фокусы становятся устойчивыми) и возникает структура с тремя предельными циклами (рис. 160, Р). Так как при Х = 0 предельных циклов нет (г/ = о - интегральная прямая, качественная структура эквивалентна структуре рис. 160, i), то рассуждениями, аналогичными проведенным в п. 3.4, находим, что при убывании X до нуля должны осуществиться следующие бифуркации сепаратрис: возникновение петли сепаратрисы вокруг верхнего фокуса, вокруг нижнего фокуса, возникновение большой петли, содержащей внутри два состояния равновесия. Так как седловая величина положительна {рх + <?и = - ф (Хд) - 1 = ;\, - 1,гдеЯ - координата точки касания иолуирямой (16) с дискриминантной кривой), то нетли сепаратрис могут быть только неустойчивыми, и их образование сопровождается влинанием в них (или, наоборот, рождением от них) неустойчивых предельных циклов. Петли сена- 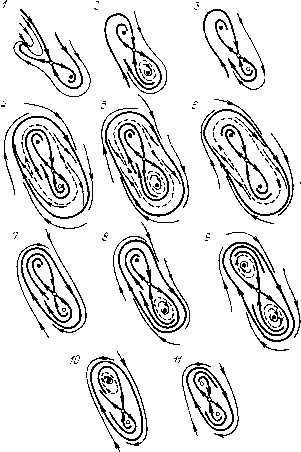 Рис. 160 ратрис вокруг фокусов возникают при влипании в них неустойчивых предельных циклов, появляющихся из фокусов. Разруще-ние большой петли, образованной аг- и cui-сепаратрисами седла, сопровождается появлением неустойчивого предельного цикла, охватывающего все состояния равновесия (большая нетля не может возникнуть за счет стягивания к ней устойчивого предель- ного цикла, так как это запрещает знак седловой величины (см. гл. 11)). Так как при X = О циклов нет, то при дальнейшем уменьшении X из слияния устойчивого и неустойчивого предельных циклов должен возникнуть двойной предельный цикл и затем исчезнуть. Точки бифуркаций на полупрямых (16), соответствующие петлям сепаратрис вокруг верхнего и нижнего фокусов, либо могут совпадать, либо должны разделяться точкой бифуркации, соответствующей большой петле. Для полупрямых (16), касающихся нижней границы дискриминантной кривой на интервалах (1, Я<°*), Я"), (Я">, Х<2>), (А,2, Xi), бифуркации будут аналогичными, но число их от интервала к интервалу будет уменьшаться за счет того, что некоторые бифуркации уже произошли нри движении вдоль дискриминантной кривой. Так как указанные бифуркации имеют место на прямых, целиком заполняющих рассматриваемую область внутри дискриминантной кривой, то существуют непрерывные кривые, на которых осуществляются бифуркации. Их начальные и конечные точки располагаются на линии симметричных структур и на дискримпнантной кривой. Все три бифуркационные кривые, соответствующие трем типам петель сепаратрис, пересекаются в точке Х=Х па линии симметричных структур (рис. 161). Они заканчиваются в точках X = = V\ Я = Х" и Я = 1 на дискриминантной кривой, в точках Я=Я2 и Я = Я"* осуществляются структуры с петлями сепаратрис. В точке Я = 1 сепаратрисы вырожденного седло-узла (см. гл. 4) нужно рассматривать как вырождение петли сепаратрисы вокруг верхнего фокуса, стягивающейся вместе с фокусом в одну точку. Кривая двойных циклов проходит между точкой Х = Х* на линии симметричных структур и точкой К = на дискриминантной кривой слева от кривой, на которой осуществляется большая нетля. Некоторые из бифуркационных кривых могут пересекаться, и поэтому последовательность качественных структур и бифуркаций при изменении параметра X вдоль отрезков касательных внутри дискриминантной крривой может быть различной. 3.6. Структуры разбиения фазового пространства и бифуркации вне дискриминантной кривой {в области одного состояния 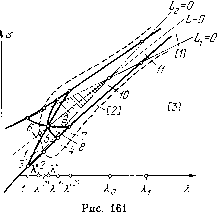 [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [ 100 ] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] 0.014 |