чивого цикла, охватывающего устойчивый фокус (рис. 215,5)). Так как а-сепаратриса при к = 0 (прямая у = а) идет в устойчивый узел в области состояние равновесия в области / ири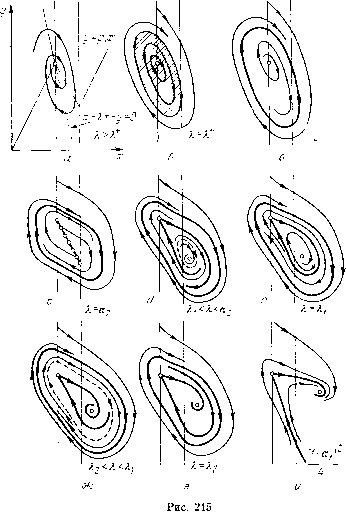

изменении параметров вдоль дискриминантной кривой устойчивости не меняет и бесконечность остается неустойчивой, то исчезновение предельных циклов на интервале О < А < аг может произойти только за счет слияния предельных циклов с последующим уничтожением двойного цикла. Это может осуществить-

ся ЛИШЬ при посредстве промежуточной бифуркации - появлении при Х = К\<а2 (рис. 215, е) петли сепаратрисы, возникшей из а- и ю-сепаратрис сшитого вырожденного состояния равновесия.

Петля сепаратрисы как снаружи, так и изнутри неустойчива. Такую петлю можно рассматривать как особый предельный цикл с состоянием равновесия на нем, отделяющий структуры с неустойчивым предельным циклом, охватывающим состояние равновесия в области /, от структур с неустойчивым циклом, охватывающим все состояния равновесия.

При убывании А до значения Х = К\ в петлю «влипает» изнутри неусточпвый предельный цикл (рис. 215, е), а прп дальнейщем убывании X и разрушении петлп от нее рождается неустойчивый предельный цикл (рис. 215, ж), охватывающий все состояния равновесия (а-сепаратриса идет в устойчивый фокус в области /, ю-сепаратриса скручивается с неустойчивого предельного цикла, который охватывает оба состояния равновесия, и между циклами нет состояний равновесия). При некотором X=X2<Xi (рис. 215, з) необходимо возникает полуустойчивый двойной предельный цикл, исчезающий при убывании X. При дальнейшем убывании X фокусы превратятся в узлы и возникнет структура, качественно эквивалентная структуре при Х = 0 (рпс. 215, и). (При убывании X до значения (1 - ai) сохраняется фокус, при дальнейшем убывании X фокус превращается в узел.)

4.3. Рассмотрим структуры внутри дискриминантной кривой при Xi<X< аг. Для значений параметров, принадлежащих самой дискриминантной кривой, для отрезков, отсекаемых а- и ю-сепаратрисами на линии сшивания, выполняется условпе (8з)а> >(5з)ш (вокруг фокуса есть неустойчивый предельный цикл), и это неравенство не может нарушиться при Х = Хо = const за счет изменения о. Оно сохраняется, в частности, и для структуры в точке пересечения X =Хо с линией симметрии о - Ххо - г/о = = О {хо, Уо - координаты середины падающего участка характеристики). В этой точке фазовый портрет симметрпчен относительно точки (хо, Уо) и, следовательно, вокруг устойчивого фокуса в области / также есть неустойчивый предельный цикл. За счет изменения о эта качественная картина внутри области, ограниченной дискриминантной кривой, не может изменпться. Отсюда следует, что при смещении с дискриминантной кривой внутрь области при разрушении сшитого вырожденного состояния равновесия появляются седло в области и устойчивый фокус в области / в сопровождении неустойчивого предельного цикла.

Структура разбиения фазового пространства при Х\ < X < аз будет содержать три предельных цикла; а-сепаратрисы седла идут к устойчивому циклу, охватывающему все три состояния равновесия; ю-сепаратрисы скручиваются с неустойчивых циклов, охватывающих фокусы в областях / и /. При Х = Х] одновременно возникают верхняя и нижняя петли сепаратрис. В них влипают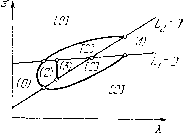

неустойчивые предельные циклы. При убывании X от значения X =Х\ из двойной петли появляется неустойчивый предельный цикл, охватывающий все состояния равновесия.

Так как при Х<{а\ - 1)/А система предельных циклов не имеет (области / п / «перечеркнуты» интегральными прямыми линейных узлов), то устойчивый и неустойчивый цпклы на интервале (ki - 1) 74 < А. < Я] должны уничтожиться. Внутри дискриминантной кривой левее отрезка петель сепаратрис должна существовать бифуркационная кривая двойных циклов. В силу упомянутой ранее симметрии кривая двойных циклов пересекает стороны дискриминаитпой кривой прп одном и том же А, = Xq.

4.4. Бифуркациоппая кривая, соответствующая слиянию устойчивого и неустойчивого циклов (кривая двойных циклов), начинается в точках, где Я = Я* на прямых Ly = а- Хх\ - у\ = О и Z,2 = о - Хх2 - г/2 = О и располагается для случая одного состояния равновесия соответственно снизу и сверху обеих прямых Z,i = О и Z,2 = О (в области L1L2 > 0). При Л = Яг обе ветви кривой двойных циклов пересекают (снизу и сверху) дискриминантпую кривую и переходят одна в другую внутри дискриминаптной кривой.

Кривая двойных циклов выделяет на интервале Х2<Х<Х в области Z,iZ,2 > О некоторую окрестность Li = 0 и L2=-0, для точек которой в фазовом пространстве есть одно устойчивое состояние равновесия и два предельных цикла.

4.5. Если состояние равновесия типа фокус лежит на падающем участке характеристики (область Ь\Ь2<0, Х>а2 на плоскости параметров), то существует единственный устойчивый предельный цикл. Существование хотя бы одного цикла очевидно (состояние равновесия и бесконечность неустойчивы). Единственность вытекает пз монотонности изменения показателя экспоненты в (4) и (5), порождаемой расположением фокуса на падающем участке характеристики (с возрастанием параметры Т] и тз растут, а тг, Т4 и 9 убывают), и дифференцируемости функции последования в точке р, сшивания.

4.6. Структура разбиен1ш пространства параметров X, о на области с различной качественной структурой фазового пространства изображена на рис. 216. Цифрами в круглых и квадратных скобках (цифры указывают на число предельных циклов) отмечены различные области. Последовательность качественных структур вдоль бифуркационной прямой Z,i == О представлена на