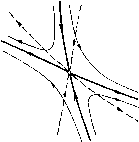Рис. 111

Если не совпадающие друг с другом м- и а-сепаратрисы одного и того же седла или различных седел системы (А) пересекают одну и ту же дугу без контакта i, то при повороте на угол одного знака их точки пересечения с дугой i сближаются, а при повороте на угол другого знака - удаляются друг от друга. При этом части одноименных сепаратрис между седлом и точкой

пересечения с дугой i до и после поворота не могут иметь общих точек.

3. Сепаратрисы системы (А), идущие из седла в седло, при повороте разделяются (различным образом при повороте на угол различных знаков). Если сепаратриса системы (А) образует петлю и в седле Ос =¥= О, то при повороте на угол одного знака она разделяется без рождения предельного цикла, а при повороте на угол другого знака она разделяется с рождением предельного цикла (см. рис. 101, 102).

4. Двойной предельный цикл при повороте на угол одного знака исчезает, при повороте на угол другого знака - разделяется на два предельных цикла (устойчивый и неустойчивый).

При повороте на угол одного знака грубый предельный цикл расширяется (содержит внутри цикл исходной системы (А)), при повороте на угол другого знака - сжимается (содержится внутри цикла исходной системы).

а) Если у исходной системы (А) существуют устойчивый и неустойчивый предельные циклы, на которых направление обхода по t одинаково (т. е. направление обхода по t па обоих циклах является направлением по часовой стрелке или на обоих- против часовой стрелки), то если при повороте на положительный (отрицательный) угол устойчивый предельный цикл расширяется, то неустойчивый сжимается, и наоборот.

б) Если у системы (А) существует два устойчивых (неустойчивых) цикла с различными направлениями обхода по t, то если при повороте один сжимается, то другой расширяется, и наоборот.

в) Если у устойчивого и неустойчивого циклов системы (А) направление обхода по t неодинаково, то при повороте эти циклы либо оба одновременно сжимаются, либо оба одновременно расширяются.

Предположим, что у рассматриваемой системы при ц. = цо существует три грубых предельных цикла, вложенных один внутрь другого: L\, Ll, Ll. Пусть Lj и Lg- устойчивые, Ll - неустойчивый. Тогда при повороте поля (происходящем, например, при возрастании (i от значения \io) при достаточно малых я пиклы L и Lg (близкие к и L") расширяются, а цикл

(близкий К Lj) сужается. Если поворот происходит на достаточно большой угол, ТО при некотором р, = p,i циклы и (или La и Lg в зависимости от того, в какую сторону поворачивается поле) могут слиться, образуя двукратный цикл, который затем при \i> Hi исчезает.

С другой стороны, пусть при [Я = Но у системы один грубый цикл L°. Предположим для определенности, что при возрастании л цикл L" расширяется. Суп];ествует такая логическая возможность: при некотором p,i > Яо из уплотнения траектории возникает двукратный цикл, содержащий L" внутри, который затем разделяется на два предельных цикла L и Lg.

§ 7. Метод малого параметра. Метод Понтрягина, Как неоднократно указывалось при качественном исследовании, вопрос об установлении существования (или отсутствия) предельных циклов является одним пз наиболее трудных вопросов; для решения его отсутствуют регулярные методы.

Поэтому любой метод, который позволяет (хотя бы для систем специального типа) устанавливать наличие предельных циклов, представляет большую ценность.

В настоящем параграфе мы изложим классические методы нахождения предельных циклов у динамических систем, близких К консервативным.

I. Системы, близкие к линейной консервативной. Рассмотрим систему

х = -у + цр{х,у,\х),

у = х + м{х,У,\),

которая при [Я = О обращается в линейную консервативную систему

у=х;

траекториями этой системы являются окружности

х2 + у2 = с.

функции р{х, у, ц) и q{x, у, р,) мы будем предполагать аналитическими функциями всех входящих в них переменных и, кроме того, такими, что

р{0, О, р)=0, q(0, О, я)=0.

(Если бы это условие не было выполнено, то, как нетрудно показать, можно заменой переменных х ж у прийти к случаю, когда оно выполняется.) Системы вида (А) часто встречаются в приложениях. Так, например, если на фазовой плоскости {х, у) {у = -х) рассматривать уравнение

х + х = \if{x, х),

Эти интегралы находятся на основании рассмотрения функции последования, построенной для системы (Ац) на какой-либо полупрямой с концом в начале координат, например, на полуоси х. Очевидно, при р, = О всякая такая полупрямая не имеет контактов с траекториями системы (Ао) (а значит, любой ее конечный кусок при достаточно малом р, не имеет контактов и с траекториями системы (Ац)), и для системы (Ао) функция последования, очевидно, будет с = с.

близкое при малых р, к уравнению гармонического осциллятора

х + х = 0,

то мы придем к системе

х = ~у, y = x-[if{x, -у),

имеющей указанный вид.

В системе (А) направление обхода траекторий по t совпадает с положительным направлением обхода. Если это не так (как в системе х = у, у = -х), то в дальнейщем нужно внести очевидные изменения.

Положим x = С cos ф, у = С sin ф; рассмотрим функцию {С):

ijj (С) = J (С COS ф, С sin ф, 0) cos ф + q{Ccos ф, С sin ф, 0)sin ф] d(p. о

После некоторых элементарных преобразований мы получим также

(0 =

= j" [рх{С COS <f, Csinф, 0) + qy {С cos <f, Csinф, 0)]d(p- .

Тогда имеет место

Теорема 1. Если для некоторого значения С = С* выполняются условия

,1, (С*) = J [р {С* COS ф, С* sin ф, 0) cos ф + о

+ q (С* cos ф, С* sin ф, 0) sin ф] dц) = О,

= [ [ря (С* COS ф, С* sin ф, 0) + qy {С* cos ф, С* sin ф, 0)] йф Ф О, о

го существуют числа г > О и 8 > О такие, что:

а) для любого [i, < б, система (Ац) имеет в г-окрестности кривой х + у = с* один и только один предельный цикл,