И Gft, для которых I является общей граничной дугой). В том случае, когда в силу заданного доопределения эти точки рассматриваются как неподвижные точки (точки покоя), они, очевидно, заполняют целую дугу (рис. 190). При сделанных предположениях относительно частных систем (Aj) и линий сщивания (системы предполагаются аналитическими и линии сшивания - также аналитическими) таких дуг неподвижных точек может существовать только конечное число.

в) В случае сшитого предельного цикла некоторые из траекторий, продолженные в силу заданного закона сшивания, могут после одной или нескольких прохождений через линии сшивания прийти в исходную точку, т. е. замкнуться.

Пусть Lo - такая сшитая замкнутая траектория (рис. 191,а). Если все траектории, проходящие через некоторую достаточно малую окрестность Lq, стремятся к Lq (т. е. при возрастании t входят и уже больше не выходят из е-окрестности Lo, сколь бы мало нп было е >0), то естественно считать Lo устойчивым пре-

Рис. 190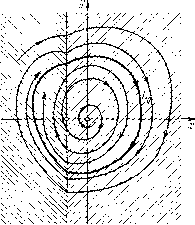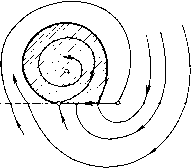

Рис. 191

дельным циклом. Очевидно, естественно может возникнуть сложный сшитый предельный цикл, в частности двукратный.

В случае, когда имеет место доопределение на линии сшивания со скачками, также, очевидно, возможен сшитый предельный цикл со скачками.

В некоторых задачах возможны предельные циклы, содержащие отрезок скользящих движений (см. рис. 191, б). В [2, 3] рассмотрен ряд задач, в которых есть сшитые предельные циклы указанных типов. Эти задачи рассмотрены путем построения точечных отображений и при этом в параметрической форме. Отметим, что рассматриваемые при этом диаграммы Ламерея состоят из двух функций соответствия.

г) Если сепаратриса состояния равновесия О пересекает линию сшивания и имеет продолжение (в силу данного доопределения на линии сшивания), то эту сепаратрису (и все ее возможные продолжения) будем называть сшитой сепаратрисой (или просто сепаратрисой) рассматриваемой сшитой системы. Сепаратриса, очевидно, является особой траекторией.

д) Пусть траектории систем (Aj) и (А), определенные в областях Gi и Gk, имеющих общую дугу сшивания Z, касаются этой дуги в некоторой точке R (в силу сделанного соглашения системы (А,) и (А) определены в областях, содержащих замыкание G, и Gfc, и, следовательно, в некоторой окрестности дуги I)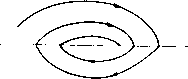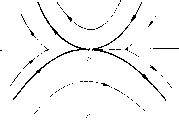

Рис. 192

п в силу доопределения на линии сшивания I эта точка считается неподвижной. Тогда мы можем получить, например, неподвижные точки типа:

1) сшитый фокус- квазифокус (рис. 192, а);

2) сшитое седло - квазиседло (рис. 192, б).

В случае 2) части траекторий, касающихся дуги I, аналогичны сепаратрисам.

В окрестности этих сшитых неподвижных точек качественная структура фазового пространства будет тождественна (в обычном смысле) разбиению в окрестности обычного фокуса и соответственно обычного седла. Однако поведение траекторий в зависимости от t, очевидно, другое (траектории стремятся к неподвижной точке О в конечное время).

е) Особой траекторией иногда естественно также считать траекторию, совпадающую целиком (или частично) с линией

склейки. Такой траекторией, в частности, является траектория скользящих движений.

Не ставя своей целью (такая цель вообще вряд ли достижима и имеет смысл) перечислить все возможные случаи доопределения, и в соответствии с этим - все возможные типы особых траекторий, приведем все же чисто геометрические примеры,

когда у сшитой системы роль особой траектории играет континуум траектории.

Так, например, отрезок особых точек (рпс. 193, я) (граничные для отрезка точки - состояния равновесия одной из систем) играет роль, аналогичную фокусу. На рис. 193, б i ° представлен случай, когда

Рис. 193 область, заполненная

замкнутыми траекториями, пграет роль элемента притяжения (очевидно, такая область может также играть роль элемента отталкивания) для других траекторий. На рис. 194 представлены некоторые возможные случаи, когда континуум траекторий, лежащий между сшитыми сепаратрисами, вместе с этими граничными сепаратрисами аналогичен сепаратрисам аналитического седла. На рис. 194, а-б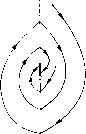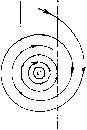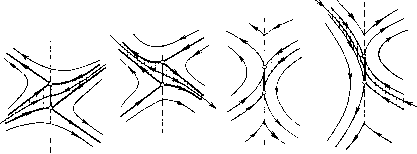

Рис. 194

представлено образование, аналогичное седлу, сшитое из двух сдвинутых аналитических седел с отрезком притяжения (соответственно отталкивания) для континуума траекторий (в обоих случаях концы отрезка притяжения (соответственно отталкивания) являются состояниями равновесия одной из сшиваемых