ВОЗМОЖНЫЕ ТИПЫ ПОЛУТРАЕКТОРИЙ

целиком лежащей в ограниченной части илоскости. Именно, это множество может быть одного из следующих типов:

I. Одно состояние равновесия.

II. Одна замкнутая траектория.

III. Совокупность состояний равновесия и траекторий, стремящихся к этим состояниям равновесия как ири f + <», так и при t - оо.

Нетрудно видеть, что состояния равновесия, входящие в множества предельных точек типа III, не могут быть фокусами или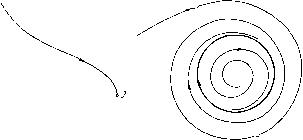

Рис. 24

узлами, так как всякая траектория, попавшая в достаточно малую окрестность такого состояния равновесия, стремится к нему и не может иметь никакой другой предельной точки. Следовательно, состояния равновесия, которые могут входить в множество точек тина III, в случае, если эти состояния равновесия простые (см. гл. 3), непременно являются седлами, а отличные от состояний равновесия траектории, входящие в это множество,- сеиаратрисами седел.

Зная возможные типы предельных множеств, мы можем сразу сказать, какие тины полутраекторий возможны. Очеврзд-по, мы получаем следующие типы: 1) состояние равновесия;

2) замкнутая полутраектория;

3) полутраектория, стремящаяся к состоянию равновесия (рис. 24, а); 4) иолутраектория, стремящаяся к замкнутой траектории (рис. 24, б); 5) иолутраектория, стремящаяся к предельному множеству тина III (рис. 25). Очевидно, во всех примерах § 12 гл. 1, кроме примеров 1 и 2, существовали траектории типа 1), т. е. состояния равновесия. Кроме того, все не являющиеся

4 Н. Н. Баутин, Е. А. Леонтович

Рис. 25

центрами состояния равновесия были со- (или а-) предельными для отличных от них траекторий. Замкнутые траектории существуют в примерах 5 и 7, причем в примере 1 замкнутая траектория изолирована (предельный цикл). В примере 7 существуют также траектории типа 4) (это все траектории, лежащие вне и внутри предельного цикла). Полутраектории типа 5) встречаются в рассмотренных далее примерах.

Приведем еще две основные теоремы, касающиеся уже не отдельной траектории, а всей совокупности траекторий в целом.

Теорема 6. Если замкнутая траектория динамической системы (А) не содержит внутри точек границы области G, то внутри нее непременно лежит хотя бы одно состояние равновесия.

Следствие 1. Внутри всякого цикла без контакта всегда существует по крайней мере одно состояние равновесия.

Следствие 2. Пусть траектория L пересекает дугу без контакта i более чем в одной точке, пусть Рх и - две последовательные по t точки ее пересечения с дугой i и С - простая замкнутая кривая, состоящая из части Р1Р2 дуги i и дуги Р1Р2 траектории L (рис. 26). Если внутри замкнутой кривой с не лежат точки границы области g, то внутри нее непременно должно лежать хотя бы одно состояние равновесия ).

Теорема 7. Пусть Р - изолированное состояние равновесия. Тогда либо в любой сколь угодно малой окрестности точки Р лежит замкнутая траектория, содержащая Р внутри себя, либо существует траектория, стремящаяся к Р {при t + <х> или при f- оо),

§ 6. Особые и неособые полутраекторип п траектории. Рассмотрение конкретных частных примеров динамических систем естественно приводит к мысли, что для знания топологической структуры разбиения на траектория нужно знать взаимное расположение не всех траекторий, а лишь некоторого конечного числа особых траекторий. В рассмотренных выше примерах такими траекториями являлись состояния равновесия, замкнутые траектории и сепаратрисы седел. Естественно возникает вопрос о том, исчерпываются ли этими типами особые траектории и как в общем случае эти особые траектории могут быть охарактеризованы. Эти вопросы рассматриваются в настоящем параграфе.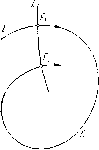

Рис. 26

) Доказательство теоремы 6 может быть проведено как с использованием понятия индекса (см. гл. 6), так и без использования этого понятия (см. [76, 12]),

) Отметим, что наличие орбитно-неустойчивых траекторий ни в какой мере не противоречит теореме о непрерывной зависимости от начальных значений, так как в этой теореме рассматривается лишь конечный промежуток значений f, а в понятиях орбитно-устойчивости и неустойчивости фигурируют все значения t от to до + оо.

Отметим, что орбитная устойчивость отличается от устойчивости по Ляпунову (см. [92, 99, 135]). Именно, траектория орбитно-устойчивая может не быть устойчивой по Ляпунову. В приводимой дальше теории особых и неособых траекторий имеет значение лишь орбитная устойчивость.

Пусть - какая-нибудь положительная иолутраектория, выделенная на траектории L. В дальнейшем рассматривается е-окрестность полутраектории. Эта окрестность, как легко видеть, непременно содержит е-окрестпость предельного множества этой полутраектории.

Определение. Будем говорить, что положительная полутраектория орбитно-устойчива, если при любом заданном е > О можно указать такое б < О, что у всякой траектории L, проходящей ири t = to через любую точку М, принадлежащую б-окрестпости М, полутраектория (точки которой соответ-

ствуют значениям t > to) целиком лежит в е-окрестпости полутраектории L+.

Справедлива следующая

Теорема 8. Если у траектории L хотя бы одна положительная полутраектория орбитно-устойчива, то всякая другая положительная полутраектория, выделенная из этой траектории, также будет орбитно-устойчивой.

Траектория L называется тогда а-орбитно-устойчивой или орбитно-устойчивой при i -> 4- оо.

Полутраектории или траектории, не являющиеся орбитпо-устойчивыми при i -> 4- оо, называются орбитно-неустойчивыми при f -> -Ь оо ИЛИ (о-орбитно-неустойчивыми.

Если траектория L орбитпо-пеустойчива при i -> -Ь оо и М - какая-нибудь ее точка, то всегда можно указать такое ео > О, что при любом сколь угодно малом б > О найдется траектория проходящая при t = to через точку б-окрестпости точки М и заведомо выходящая при некоторо-м i = Г из Ео-окрестности иолутраектории L).

Все сказанное относительно положительной полутраектории с очевидными изменениями может быть повторено и относительно отрицательной полутраектории. Таким образом, мы будем также говорить о траектории, орбитно-устойчивой ири t - <х>, или а-орбитно-устойчивой, и о траектории, орбитпо-пеустойчивбй при t - °°, или а-орбитпо-пеустойчивой. Траектория L, орбитно-устойчивая как при t + °°, так и при t - °°, называется просто орбитно-устойчивой ИЛИ неособой. Всякая траектория, не являющаяся орбитно-устойчивой, называется орбитно-неусгойчивой ИЛИ особой. Кроме того, особой траекторией будем считать и всякое состояние равновесия ").