§ 8] НАПРАВЛЕНИЕ НА ТРАЕКТОРИЯХ 19

«изображающая точка, двигаясь по L при возрастании t, пересекает данную дугу», «входит в данную область», «стремится к состоянию равновесия» и т. д. или «траектория при t = to пересекает данную дугу», «входит в данную область» или «стремится при t +00 -оо) к состоянию равновесия» и т. д.

Состояние равновесия (особая точка) М{а, Ь) системы (А) называется изолированным {изолированной), если существует окрестность точки М{а, Ь), в которой, кроме М, не лежит больше ни одного состояния равновесия.

Если все точки кривой являются состояниями равновесия (особыми точками), т. е. во всех точках этой кривой Р{х, у) = Q{x, У)=, то такая кривая называется особой линией системы (А).

В некоторых статьях п монографиях (в основном классических, например у Пуанкаре и Бендиксона) вместо установившегося в настоящее время термина «траектория» используется термин «характеристика».

§ 7. Теорема о непрерывной зависимости решения от начальных условий. Кроме теоремы 1 (о существовании и единственности решения) основной теоремой, описывающей свойства решений, является теорема о непрерывной зависимости от начальных условий. Мы сформулируем ее применительно к системе (А) в следующей геометрической форме.

Теорема 5. Пусть Мо{хо, уо) и Mi{xu у\)-две точки одной и той же траектории L, соответствующие [при некотором выборе движения на L) значениям t = to и t = t\.

Тогда для любого е > О можно указать т) > О такое, что всякая траектория L, при t = to проходящая через какую-либо точку М ц-окрестности точки Mq, определена при всех значениях t, totti, и при t = ti проходит через некоторую точку Mi окрестности точки М\; каждая точка траектории L, соответствующая какому-либо значению t, tot ti, лежит в е-окрестности точки траектории L, соответствующей тому же значению t).

§ 8. Направление на траекториях. Изменение параметризации.

Как уже было сказано, на всякой траектории L вводится определенное направление в качестве положительного (именно направ-

•2) Отметим тот частный случай, когда траектория L является состоянием равновесия О (в этом случае при всех t мы получаем одну и ту же точку О, так как вся траектория является точкой). Тогда из теоремы о непрерывной зависимости от начальных значений имеем: какой бы промежуток значения t, tot ti, мы ни взяли, при всяком е > О найдется Т1 > О такое, что всякая траектория, проходящая при t = tg через ti-ok-рестность состояния равновесия О, в течение значений t,tot ti, не выйдет из 8-окрестности О, т. е., грубо говоря: «чем ближе траектория к состоянию равновесия, тем дольше она около него находится».

Очевидно, что при переходе от системы (А) к (А*) направления на траекториях остаются неизменными, если f{x, у)> О, и меняются, если f{x, у)<0.

*) Пользуясь кинематической интерпретацией, т. е. считая t временем, можно сказать, что положительное направление на траектории L есть то Hfi-правление, в котором точка М(ф(*), ij)(f)) (x=cp{t), !/ = i)(f) - решение, соответствующее траектории L) движется по траектории с возрастанием t.

ленив в сторону возрастания 0)- Введенное таким образом направление не зависит от того, какое из решений, соответствующих траектории L, мы возьмем (так как все такие решения получаются одно из другого заменой ? на t + с). Рассмотрим наряду с системой (А) систему

х-Р{х, у), y = -Q{x, у). (А)

Векторное поле системы (А) получается из векторного поля системы (А), если изменить направление каждого вектора на про-тивоположное (не меняя длин векторов). Непосредственной проверкой устанавливается, что каждому решению

x==q,{t), г/ = ф(0 системы (А) соответствует решение

X = (f,{ - t), у = ф( -/)

системы (А). Отсюда очевидно, что системы (А) и (А) имеют одинаковые траектории, но индуцируют на траекториях противоположные направления. Таким образом, переход от системы (А) к системе (А) можно рассматривать как изменение параметризации на траекториях, именно как замену параметра t параметром -t.

Рассмотрим более общий случай изменения параметризации. Пусть f{x, у) - аналитическая функция, определенная в той же области плоскости, что и функции Р{х, у) и Q{x, у), и пусть функция f{x, у) отлична от нуля во всех точках, отличных от состояния равновесия системы (А) (и имеет один и тот же знак). Рассмотрим наряду с системой (А) систему

dx/ds-P*{x,y) = P{x,y)f{x,y),

dy/ds = Q*{x, y)=Q{x, y)f{x, у). >

Можно показать, что системы (А) и (А*) имеют одни и те же траектории, но с различными параметризациями на них. Именно, можно показать, что между параметрами t п s существует следующая зависимость:

Предположим теперь, что функция f{x, у) может обращаться в нуль в точках, отличных от состояний равновесия системы (А), а также может менять знак в области G. Рассмотрим снова систему (А*). Очевидно, что состояниями равновесия системы (А*) являются все состояния равновесия системы (А), а также все точки области G, которые не являются состояниями равновесия системы (А), но в которых f{x, г/)= 0.

Кривая

/К У)=0

будет особой линией системы (А*) (каждая точка этой кривой является состоянием равновесия системы (А*)).

Рассмотрим теперь траекторию L системы (А), отличную от состояния равновесия. Если на траектории L функция f{x, у)Ф Ф О, то, так же как и выше, L является траекторией системы (А*) с измененной, вообще говоря, параметризацией. Если же на траектории L имеются точки S\, S2, S3 кривой f{x, г/)=0, то все точки L, отличные от этих точек, распадаются, как легко видеть, на конечное или счетное число гладких кривых, являющихся траекториями системы (А*) (рис. 4). Направление на

f(x.i/H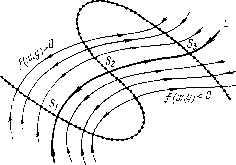

Рис. 4

каждой такой траектории совпадает с направлением на L, если на этой траектории f{x, у)>0, и не совпадает в противном случав.

Таким образом, каждая траектория системы (А) либо является траекторией системы (А*), либо состоит из конечного или бесконечного множества траекторий системы (А*).

В приложениях часто встречаются динамические системы вида

Р {X, У) f (X, у)

Q (д, у) f {X, у)

(А**)