бым системам на рис. 173, помеченным двумя цифрами, соответствуют бифуркационные кривые рпс. 174, разде.тяющпе соответствующие области.

5. Качественные картины и возможные бифуркации при р = 1 и р > 1, При возрастании f> до значения f> = 1 состояния равновесия сливаются. Структура разбиения пространства параметров для f> = 1 будет такая же, как на рпс. 174. Соответствующие структуры разбиения фазового пространства будут отличаться от структур для случая О < < Р < 1 лишь тем, что на осп ф будет одно состояние равновесия типа седло-узла.

Прп возрастании f> от значения f> = 1 при а и S, взятых пз области 2 рис. 174, исчезает состояние равновесия седло-узел. При значениях а и s, взятых пз областп 1, происходит появление устойчивого предельного цикла из а-сепаратрпсы сед-.т10-узла. На плоскости параметров при этом исчезает бифуркационная кривая L.

§ 7. Частотно-фазовая автоподстройка частоты (случай существования трех предельных циклов). Рассмотрим систему рас-сматривавщуюся в гл. 15 методом малого параметра (фазовое пространство - цилиндр) [44]:

Рис. 174

Ч> = У, У = Р - sin ф - Яг/ - 2as

S -i-U

Известными методами качественной теории обнаруживается, что для всех значений параметров а>0, s>0, Я>0, 0<f><l на оси = 0 есть два состояния равновесия: Oi (arcsin р, 0) - устойчивый узел пли фокус, Ог (я - arcsin f>, 0)-седло. Траектории на нижнем полуцилиндре идут пз бесконечности на верхний полуцилиндр. На нижнем полуцилиндре и вокруг точки Oi циклов нет (см. § 6). Все бифуркации могут происходить только на верхнем полуцилиндре.

Для больщих Я структура разбиения фазового пространства однозначно определяется сравнением с системой

Ф=г/, г/= Р - sin ф - 2хг/. (2)

Как известно (гл. 20, § 4), для каждого f> (0<f><l) существует такое х*(Р), что при и > и* м-сепаратриса седла систе мы (2), выходящая на верхний полуцилиндр, не пересекает = О и уходит В бесконечность на верхнем полуцилиндре. Если Я>2и, то поле направлений (1) повернуто относительно поля направлений (2) по часовой стрелке. Поэтому, если %> %* и Я>2и, то м-сепаратриса седла системы (1) также должна идти

в бесконечность. Циклов нет. Структура разбиения фазового пространства эквивалентна представленной на рис. 175,0.

Проследим за изменением качественной структуры и возможными бифуркациями при фиксированных (0<р<1) и s>0 в плоскости параметров (а, X). Качественная структура не будет зависеть от выбранных и s. Качественные структуры, осуществляющиеся вдоль прямой Я = О, известны (см. § 6). Существуют такие ai п аг, что на куске О < а < ai (р, s) оси а будет осуществляться структура разбиения без предельных циклов.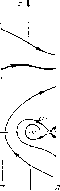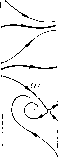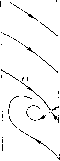

Рис. 175

На куске ai(p, s)<a<a2(f>, s)-структура с двумя предельными циклами на верхнем полуцилиндре (нижний - устойчивый, верхний - неустойчивый). На куске а2(Р, s)<a<oo - структура с одним неустойчивым предельным циклом. Точке а = = ai (Р, s) соответствует структура с двойным предельным циклом, возникшим пз сгущения траекторий. Точке а = аг(Р, s) - структура с петлей сепаратрисы, охватывающей верхний полуцилиндр. Проследим за сменой качественных структур и возможными бифуркациями при возрастании % вдоль прямых а = ао. Рассмотрим три случая.

1. ао>а2. При возрастании X от значения Я = 0 в уравнении появляется член -Ху и бесконечность становится неустойчивой. Из бесконечности появляется устойчивый предельный цикл. Эта структура изображена на рис. 175, 2. На верхнем полуцилиндре два предельных цикла. При возрастании X поле направлений поворачивается по часовой стрелке и предельные циклы монотонно сближаются (устойчивый опускается, неустойчивый поднимается). Так как при Я > и* заведомо осуществляется структура разбиения, представленная на рис. 175,0 (циклов уже нет), то существует такое Я = Я++(а; s), для которого

предельные циклы сливаются, образуя двойной полуустойчивый предельный цикл. При возрастании "к от бифуркационного значения двойной предельный цикл исчезает.

2. ai < ао < аг. При возрастании к от значения Я = О из бесконечности появляется третий предельный цикл (устойчивый). Эта структура изображена на рис. 175,3. При возрастании к верхний п нижний устойчивые предельные циклы монотонно опускаются, а расположенный между ними неустойчивый - монотонно поднимается. Так как при к> %* циклов нет, а поле поворачивается с возрастанием к монотонно, то существуют Я = Я*(а; s), соответствующее слиянию неустойчивого предельного цикла с верхним устойчивым, и к = ко{а; f>, s), соответствующее влипанию нижнего устойчивого цикла в петлю сепаратрисы на верхнем полуцилиндре (петля может возникнуть только при стягивании к петле устойчивого предельного цикла, так как седловая величина Р(р + Qy = - {2a/s + к) отрицательна).

3. О < ао < аь При возрастании к от значения к = 0 из бесконечности появляется устойчивый предельный цикл, который с возрастанием к монотонно опускается. Так как при к> %* циклов нет и седловая величина отрицательна, то существует к = ко{а; р, s), соответствующее петле сепаратрисы седла на верхнем полуцилиндре. При к = ко устойчивый предельный цикл влипает в петлю сепаратрисы.

Если монотонный поворот поля не повсюду увеличивает шаг спиралей, охватывающих цилиндр (расстояние между витками), то остается еще возможность возникновения двойного предельного цикла из сгущения траекторий с последующим разделением двойного цикла на простые - устойчивый и неустойчивый. Такая возможность действительно реализуется при возрастании к вдоль прямой a = ao<ai, если ао достаточно близко к аь

Точке {к = 0, a = ai) соответствует структура разбиения фазового пространства с двойным полуустойчивым предельным циклом на верхнем полуцилиндре. Так как поле направлений поворачивается в противоположных направлениях при возрастании к и нри убывании а (соответственно по и против часовой стрелки), то предельный цикл при возрастании к разделяется на два, а при убывании а исчезает. Из соображений непрерывности следует, что на плоскости (а, к) существует бифуркационная кривая Я, = Л,+ (а; s), выходящая из точки (Я = 0, a = ai) с отрицательным наклоном, для которой двойной цикл не разрушается. Прямая a = ao<ai эту кривую пересекает, если ао достаточно близко к аь

Проследим за изменением качественных структур при возрастании к вдоль прямой а = ао < ai при ао, достаточно близком к аь При к = 0 будет осуществляться структура рис. 175,0. Циклов нет. При переходе к положительным к появляется устой-