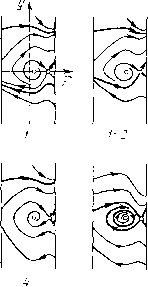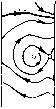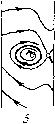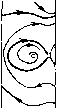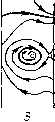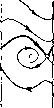Рис. 178

или узел. Предельные циклы вокруг состоянпя равновесия не могут существовать прп ]d\ < 1, так как здесь Р + Qy = - А (1 - d cos ф) 0. Качественная картина фазового пространства для достаточно больших % на любой кривой %d = k представлена на рпс. 178, 6. i- м "о

торий системы (1), то должно быть

J [y - X{\ - d COS ср) у] d(f = 0.

Но это невозможно нри г/(ф)<0, li(< 1 п положительных Я и Y. При liil < 1 состояние равновеспя Oi - устойчивый фокус

4, Качественные картины фазового пространства и возможные бифуркации нри малых f. Рассмотрим случай d>0. Условие

грз (1) = 2лV--з~ - 3) = О при малых и X дает в плоскости

(X, d) асимптотическое представление кривой, выделяющей область плоскости параметров, соответствующую качественной структуре, представленной на рис. 178,.?. Для А;<(3/4)л кривые не входят в область, выделяемую условием (5). Для к> >(3/4)л существуют fc-кривые, принадлежащие своей частью к области, выделяемой требованием малости величин f, Х и Kd и. соединяющие области пространства параметров, соответствующие структурам разбиения, представленным на рис. 178,2 и 178,6.

Нетрудно обнаружить, проследив за появлением предельных циклов из бесконечности при малых f и X, что любая fc-кривая, не принадлежащая к области Ы < е, также соединяет области пространства параметров, соответствующие структурам фазового пространства на рис. 178,2,6 (приложение I). Изменение параметров X ш d вдоль /с-кривых осуществляет монотонный поворот векторного поля.

Проследим за поведением при этом сепаратрис седла. Для структуры разбиения фазового пространства, представленной на рис. 178,2, на прямой ф = фо, проходящей через точку Oi, отметим ближайшие к седлу точки пересечения с а- и со-сенаратри-сами: Pi на а-сепаратрисе на нижнем полуцилиндре, Рг на (о-сепаратрисе на нижнем полуцилиндре, Ps на а-сепаратрисе

на верхнем полуцилиндре, Р4 на со-сепаратрисе на верхнем полуцилиндре и Рз - вторую точку пересечения на (о-сепаратрнсе, идущей к состоянию равновесия Oi (рис. 179). При возрастании X вдоль fc-кривых поле направлений поворачивается по часовой стрелке и точки Pi и Р4 монотонно поднимаются, а точки Рг, Рз и Р5 монотонно опускаются. Возможные бифуркации соответствуют совпадению сначала точек Рг и Pi, после этого точек Рз и Pi, а также точек Р4 и Ps- Эти бифуркации действительно осуществляются, так как при возрастании X вдоль fc-кри-вых происходит переход от структуры, представленной на рис. 178, 2, к структуре, представленной на рис. 178, 6, п при этом разности координат уъ~у\ и уь - уА меняют знак (индексы при координатах соответствуют индексам точек).

Множества точек на плоскости {X, d), для которых осуществляются совпадения точек Рг и Pi (существует петля сепаратрисы снизу), Рз и Pi (существует петля вокруг точки Oi) или Р4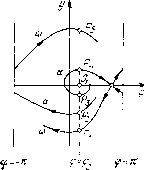

Рис. 179

и Ръ (существует нетля сверху), образуют бифуркационные кривые L", L° и i/", разделяющие плоскость {К, d) на области, для которых качественные структуры различаются поведением сепаратрис седла. Поведение сепаратрис с точностью до четного числа предельных циклов определяет структуру разбиения фазового пространства на траектории.

Уравнение 11)2(1) = О дает для малых f ж К асимптотическое представление i/-кривой; L-кривая (та ее часть, которая соответствует dO) начинается на оси d = 0 (при d = 0 для малых и для больших Я будут соответственно существовать структуры рис. 178, 4, 6; при возрастании Я поле монотонно поворачивается и, следовательно, существует единственное бифуркационное значение, соответствующее точке L-кривой).

Кривая LP располагается между L- и Для малых и Я кривая L° представляется уравнением d = 3 (см. гл. 15, § 2). Кривые L~, L° ж L с каждой из fc-кривых пересекаются в одной точке и уходят в бесконечность. Они не могут пересекаться, так как при > О и любых К ж d же может осуществляться структура разбиения на траектории, при которой сепаратрисы седла образуют две петли на нижнем и верхнем полуцилиндрах (такой структуре соответствовала бы точка, в которой пересекаются три кривые L~, L° ж L*).

Если предположить, что такая структура при некотором > О осуществляется, то при убывании в силу монотонности поворота векторного поля на верхнем и нижнем полуцилиндрах (соответственно по и против часовой стрелки) обе петли разрушаются и возникает структура, в которой и на нижнем, и на верхнем полуцилиндрах а-сепаратриса располагается ниже со-сепаратрисы. Только от такого расположения сепаратрис может появиться при возрастании "f двойная петля, образованная сепаратрисами седел. При = О и любых X ж d такого расположения сепаратрис не может быть из-за симметрии поля направлений относительно начала координат; и при возрастании "f оно не может возникнуть, так как из-за различного направления поворота поля на нижнем и верхнем полуцилиндрах при возрастанип f точки а-сепаратрис на каждом полуцилиндре могут только подниматься, а точки со-сепаратрис - только опускаться.

Из сказанного следует, что при возрастании X вдоль fc-кри-вых, соединяющих структуры, представленные на рис. 178,1,6 (А; > (3/4)л), осуществляется такая последовательность бифуркаций, при которой сначала сливаются точки Р2 и Pi, затем точки Рз и Р] и, наконец, точки Р4 и Р5. Кривые Ь+ и Oi = О пересекаются (это следует из асимптотического представления Z/"*" - кривой уравнением i)(l)=0), и поэтому при движении вдоль к-кривых стягивание предельного цикла к точке (при пересечении линии О] = 0) может как предшествовать стягиванию предельного цикла к петле сепаратрисы (при пересечении кривой Z,*),