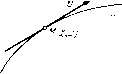В каждой точке М(х, у) траектории L, не являющейся особой точкой векторного поля, вектор v с компонентами Р(х, у), Q{x, у) является касательным вектором к траектории L (рис. 1).

Пусть Л/о(й, Ь)- особая точка системы (А), так что Р{а, b) = Q{a, Ь)=0.

Тогда очевидно, что

х = а, у = Ъ

есть решение системы (А), и, следовательно, особая точка сама является отдельной траекторией. Такая траектория называется состоянием рав-yk. новесия.

На траекториях, отличных от состояний равновесия, естественным образом вводится положительное направление движения, именно движение в сторону возрастания t. В каждой точке траектории это направление дается соответствую-Рис. 1 щим касательным вектором х =*

Р(, У), У = Q{x, у). Приведем следующие два основных предложения. Лемма 1. Пусть траектория L, соответствующая решению (3), на интервале x<t<T отлична от состояния равновесия, и пусть существуют значения t\ и (т < < 2 < Т) такие, что

Ф(Й)=Ф(2), {tx)=W2)-

Тогда решение (3) определено при всех значениях t (т. е. f = -оо, Т=+оо) функции ф(0 и t>(i) являются периодическими функциями t, а соответствующая траектория - простой гладкой замкнутой кривой.

(В силу этого предложения никакая траектория не может « самопересекаться ».)

Лемма 2. а) Всяки.ч двум решениям, отличающимся только выбором начального значения to, соответствует одна и та же траектория, б) Всякие два различных решения, соответствующие одной и той же траектории, отличаются друг от друга только выбором начального значения to.

Замечание. Все решения, соответствующие данной замкнутой траектории, являются периодическими решениями с одним и тем же периодом.

На основании лемм 1 и 2 без труда устанавливается

Теорема 4. Через каждую точку области G {или плоскости) проходит одна и только одна траектория.

§ 5]

СОПОСТАВЛЕНИЕ ГЕОМЕТРИЧЕСКИХ ИНТЕРПРЕТАЦИЙ

Таким образом, задавая в области G (которая может совпадать со всей плоскостью) динамическую систему (А), мы тем самым задаем некоторое семейство траекторий, или, в другой терминологии, разбиение этой области (или плоскости) на траектории.

§ 5. Сопоставление геометрической интерпретации системы (А) в пространстве {x,y,t) с интерпретацией на фазовой плоскости, а) В каждую траекторию проектируется бесчисленное множество интегральных кривых пространства {х, у, t), получающихся друг из друга заменой t иа t - с (или, что то же, проходящих через точки с одними и теми же координатами хо, уо и различными to). Каждая такая интегральная кривая соответствует некоторому решению, соответствующему траектории (рис. 2).

б) Если а, 6 - значения, для которых Р{а, Ь)=0, Q{a, b) = 0, то интегральная кривая пространства {х, у, t), проходящая через точку с координатами а, Ь, to, где to любое, очевидно, является прямой, параллельной оси t; эта прямая проектируется на плоскость {х, у) в единственную точку М{а, Ь), которая, очевидно, является состоянием равновесия системы (А) ").

в) Если решение - периодическое с периодом т, то в пространстве {х, у, t) соответствующая интегральная кривая есть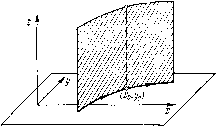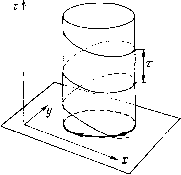

Рис. 2

Рис. 3

спираль с шагом т. Эта спираль проектируется на плоскость {х, у) в замкнутую кривую (рис. 3).

") Отсюда очевидно, что ни в одной точке интегральной кривой пространства (х, у, t), отличной от соответствующей состоянию равновесия, касательная не может быть параллельна оси t (т. е. ни в одной точке, отличной от состояния равновесия, траектории ф(*) и tf(t) не могут одновременно обращаться в нуль, в противном случае мы получили бы противоречив с теоремой о существовании и единственности решения).

2 Н. и. Ваутин, Е. А. Леонтович

В динамических системах, возникающих из приложений, t часто имеет смысл времени. Однако при этом следует подчеркнуть, что «траектории», о которых речь идет в тексте, являются «фазовыми траекториями» (траекториями на фазовой плоскости), а не траекториями движения.

Из теоремы существования и единственности решения вытекает, что точка M{(f{t), {t)), при изменении t двигающаяся по некоторой траектории L, не может стремиться к точке какой-либо отличной от L траектории при t, стремящемся к конечному значению (в противном случае интегральные кривые в пространстве {х, у, t) пересекались бы, что невозможно в силу теоремы 1).

В частности, точка, двигаясь по траектории, отличной от состояния равновесия (отличной от замкнутой траектории), может неограниченно приближаться к состоянию равновесия (замкнутой траектории) либо при t -> +°о, либо при t- -°о.

Состояния равновесия и замкнутые траектории являются траекториями, представляющими наибольший интерес для приложений. Состоянию равновесия соответствуют состояния равновесия той физической системы, которая описывается данной динамической системой, а замкнутые траектории соответствуют периодическим движениям - колебаниям, автоколебаниям.

§ 6. Некоторые термины. Если решение, соответствующее данной траектории L, определено для всех значений t, -<» < t< 4-оо, то траекторию L иногда называют целой траекторией.

Если Мо - точка траектории L, которая при выбранном на L движении соответствует значению t - to, то множество точек L, соответствующих значениям fta (или же tto), называется положительной полу траекторией (соответственно отрицательной полутраекторией), выделенной из L, и обозначается соответственно через L" (или L~).

Когда траектория L является состоянием равновесия или замкнутой траекторией, всякая положительная и всякая отрицательная полутраектории, выделенные из нее, очевидно, совпадают с ней самой. Полутраектория, выделенная из незамкнутой траектории, называется незамкнутой полутраекторией, траектория, выделенная из замкнутой траектории (в силу сказанного выше совпадающая с ней),- замкнутой. Параметр t часто называется временем, а решение системы {К) - движением, соответствующим траектории, или движением по траектории {кинематическая интерпретация динамической системы)2). Точка Л/(ф(), г)()) называется изображающей точкой.

Используется следующая терминология: «изображающая точка при t = tu проходит через данную точку Мо траектории L», или «траектория L при t = to проходит через точку Л/о», а также