Знания одного только числа к* к* = lim j еще недостаточно для того, чтобы определить, в каком именно направлении полутраектория L"*" стремится к состоянию равновесия О. Действительно, соотношению tg 0* = = к* (О<0*<л) удовлетворяют два (взаимно противоположных) направления.

В дальнейшем при рассмотрении сложных состояний равновесия мы часто будем говорить об отыскании траекторий, стремяп];ихся к состоянию равновесия с Рис. 40 угловым коэффициен-

том, или наклоном, к*. При этом мы будем иметь в виду как траектории, стремяп];иеся к рассматриваемому состоянию равновесия в направлении 9*, так и траектории, стремяп];иеся в направлении л + 9* (0<9*<л, tg0* = A;*).

Поставленный выше вопрос о суп];ествовании для луча ОМ предельного положения ОМ* можно рассматривать как вопрос о суп];ествовании касательной в точке О у кривой, представляюп];ей собой траекторию L, дополненную точкой 0). Наряду с этим можно рассматривать вопрос о существовании предельного положения касательной к траектории L в точке il/(i) (npni-+oo).

Можно показать, что в случае, когда они существуют, они совпадают (см. также § 4).

Для кривых, не являющихся траекториями, данное утверждение, вообще говоря, несправедливо. Рассмотрим, например, кривую, заданную уравнениями

г/sin(l/x) при х¥=0, у = 0 при x = 0.

Эта кривая имеет касательную в каждой точке, в том числе с абсциссой x = О, однако касательная в точке М с абсциссой х не стремится, как легко видеть, ни к какому предельному положению при X 0.

) При этом касательную надо понимать как предельное положение секущей ОМ при t -f оо. Это замечание приходится делать ввиду того, что траектория L, дополненная точкой О, не является кривой, заданной параметрически (точка О не соответствует никакому значению *)•

дел отношения y{t)/x{t), причем этот предел равен tg 9*: Iim4 = tg9* = i*.

Предположим, кроме того, что рассматриваемое состояние равновесия не центр, так что сугцествует полутраектория x = x{t), y = y{t) при i+00 (- оо), стремяш;аяся к состоянию равновесия 0(0, 0).

Тогда dy/dx имеет предел при t +оо (конечный или бесконечный) в том и только в том случае, когда имеет предел y(t)/x{t), причем в случае существования этих пределов они равны, т. е.

lim 4= ]im-i = A;.

dx f X {t)

При этом угловой коэффициент к удовлетворяет соотношению

т. е. квадратному уравнению

bk+{a~d)k-с = 0. (13)

При этом, если 6 = 0, то одним из корней этого уравнения считается оо, т. е. одно из направлений, по которому траектории стремятся к состоянию равновесия О, есть направление оси у.

Отметим, что дискриминант квадратного уравнения (13) совпадает с дискриминантом характеристического уравнения. Поэтому в случае, когда этот дискриминант отрицателен, т. е. в случае фокуса (простого или сложного), не существует направлений, в которых траектории могут стремиться к состоянию равновесия. Нетрудно показать, что корни уравнения (13) ki и к2 связаны с характеристическими корнями Я] и Яг соотношениями

h=i%i - a) /Ъ, кг = (Яг - а) /Ъ.

Приведем результаты, касающиеся простых состояний равновесия в предположении, что в окрестности простого состояния равновесия система приведена к каноническому виду.

1. а) Характеристические корни действительны, различны и одинаковых знаков (узел). Система приводится к каноническому виду

dx/dt = Xxx +(f{x, у), dy/dt = k2y- {х, у). .(14)

§ 7. Угловое коэффициент направления, в котором траектория может стремиться к простому состоянию равновесия. Запишем рассматриваемую систему в виде

dxjdt = ах + by + ф(х, у), dy/dt = сх + dy + it>(x, у) (А)

(ф(> у) и it)(x, у)-ряды, начинаюп];иеся со степеней х и г/ не ниже второй), и при этом

а Ъ

с d

В этом случае в уравнении (13) мы имеем 6 = 0, с = 0, а - d = = Xi - Хг О, и, следовательно, существует два значения к (напомним, что при & = 0 мы считаем один корень равным °°), Предположим для определенности, что < Xi < О (устойчивый узел).

Все траектории системы (14) стремятся к состоянию равновесия О в определенных направлениях, и этими направлениями являются л/2 и Зл/2, О и л. При этом в направлениях л/2 и Зл/2 стремятся только но одной траектории). Все остальные траектории стремятся к узлу в направлениях О и л, причем в каждом из этих направлений стремится бесчисленное множество иолутраектории (рис. 41).

Соответствующим образом измененное утверждение имеет место для случая Xi < Хг < О, а также для случая, когда О - неустойчивый узел (О < Xi < Хг или 0<Хг<Х1).

б) Характеристические корни равны (Х1=Хг = Х), и система может быть приведена к каноническому виду

dxldt = Хж + ф (ж, у),

(15)

dyldt = Хг/ + 1; (ж, у).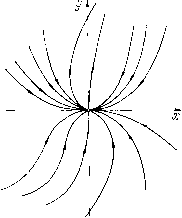

Рис. 41

В этом случае узел называют дикритическим. В уравнении (13) & = с = а - d = 0. В этом случае каждая траектория системы (15), стремящаяся к узлу О (ири t-+oo, если X < О, и при i- оо, если Х>0), стремится к нему в определенном направлении, причем для любого направления имеется в точности одна соответствующая ему иолутраектории (рис. 42).

в) Характеристические корни равны (Х1 = Хг = Х), и система может быть приведена к виду

йж/Л = Хж + ф(ж, у), dyldt = Ху + цх + ){х, у), (16)

В этом случае узел иногда называется вырожденным. В этом случае в уравнении, определяющем угловые коэффициенты направлений

bk+{a-d)k + cO, как нетрудно видеть, Ь = а - d = 0, с = р=70; оба корня этого

*) Доказательство этого утверждения может быть проведено различными способами. См., например, [12, 130].