
 |
|
Главная страница Приемы качественного исследования [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [ 14 ] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] S 3] ПРЕДЕЛЬНАЯ ТОЧКА ПОЛУТРАЕКТОРИИ Рассматривая либо параметрические уравнения простой замкнутой кривой С, либо ее уравнения в декартовых координатах, можно аналитически записать условия того, что рассматриваемая замкнутая кривая С является циклом без контакта, полностью аналогичные условиям (1) и (3). В некоторых случаях роль цикла без контакта может играть «обобщенный цикл без контакта» или «цикл однократного пересечения». Мы скажем, что простая замкнутая кривая С (эта кривая может и не быть гладкой) есть р цикл однократного пересечения ддя траектории системы (А), если: а) на кривой С не лежит ни одно состояние равновесия; б) у всякой траектории, ири t = to проходящей через какую-нибудь точку кривой С, точки, соответстующпе достаточно близким к to значениям t > to{t < to), лежат внутри С, а точки, соответствующие достаточно близким к t значениям t <to{t> to),- вне цикла С. В частности, например, гладкая простая замкнутая кривая, не являющаяся циклом без контакта, является циклом однократного пересечения в том случае, когда в некоторых своих точках) она имеет точки сокрикосновения четно-г о порядка с траекториями, и во всех других точках не имеет контакта. Очевидно, если цикл однократного пересечения является гладким и F{x, у)=0 - его уравпепие, то в точках этого цикла выражение F; (аг, у) Р {X, у) + Fy {х, у) Q {X, у) может обращаться в нуль. § 3. Предельная точка полутраектории и траектории. Предельная траектория). Будем рассматривать только такие полутраек- 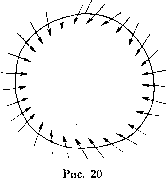 5) Траектории не могут касаться гладкой замкнутой кривой во всех ее точках, так как в этом случае кривая также была бы интегральной кривой. Это невозможно, так как по предположению для рассматриваемой динамической системы выполняются условия теоремы существования и единственности. ) Термин «предельная точка» употребляется также в теории множеств. Именно, точка М*, принадлежащая или не принадлежащая данному множеству К, называется предельной точкой или точкой сгущения множества К, если сколь угодно близко от точки М* лежат точки К, отличные от М*. Понятие предельной точки полутраектории имеет другой смысл. Например, состояние равновесия является предельной точкой д.чя самого се- бя - в смысле данного в тексте определения, но не является предельной точкой в смысле теории множеств, так как в этом слзгчае множество К состоит из одной единственной точки (состояния равновесия). Во избежание путаницы всюду в дальнейшем вместо термина «предельная точка»- в смысле теории множеств - используется термин «точка сгущения». тории и траектории, которые целиком лежат в ограниченной части плоскости. Из теоремы 2, очевидно, следует, что на всякой такой положительной (отрицательной) полутраектории любое решение определено для всех значений t>tQ {t<to), где to - некоторое (зависящее от выбора решения) фиксированное значение. На всякой траектории, целиком лежащей в ограниченной части плоскости, всякое решение определено для всех значений t, - °о < t < + °о. При рассмотрении возможного поведения отдельной полутраектории вводится понятие «предельной точки полутраектории». Точка М* называется предельной точкой положительной полутраектории (или соответственно отрицательной полутраектории Ь~), если при любом сколь угодно малом е>0 и любом сколь угодно большом Г > О (любом Г < 0) в круге радиуса е с центром в точке М* лежит хотя бы одна точка полутраекторни {L~), соответствующая значению t>T (или соответственно t<. Т). Из определения предельной точки полутраектории непосредственно следует, что если \*, г* - координаты предельной точки М* положительной иолутраектории л; = ф(), г/= \fi(i) - решение, соответствующее то существует последовательность неограниченно возрастающих значений t tu h, t„ (i„ -> + °o ири re -> + 0°) таких, что lim Ф{tn) = I*, lim ij)(tn) = Ti*. (4) Обратно, из существования последовательности неограниченно возрастающих значений i„, для которой выполняются условия (4), следует, что точка М*{%*, ц*) есть предельная точка полутраектории L. Точка М называется предельной точкой целой траектории L, если М есть предельная точка либо для положительной полутраектории либо для отрицательной полутраектории L~, выделенной из траектории L (в первом случае точку М часто называют (и-пределъной точкой, во втором - а-пределъной точкой траектории L). Предельная точка траектории L может как принадлежать самой траектории L, так и не принадлежать ей. Примеры. 1) Всякое состояние равновесия О {а, Ъ) является своей единственной предельной точкой (как со-, так и а-иредельной), так как в этом случае при всех t х = а, у = Ъ. 2) Все точки замкнутой траектории, очевидно, также являются ее (О- и а-иредельными точками. Действительно, соответствующее замкнутой траектории L движение x = ff{t), y = {t) является иериодическим (с некоторым периодом Го), и каждая точка М(%„ г) этой траектории соответствует бесчисленному множеству значений Р. = т, 2 = т + Го, ..., = т -f(re - 1) Го, ..., а также 1 = т, 2 = т - Гц, ..., = т - (и - 1) Г„, ... Согласно определению она является, следовательно, как со-, так и а-предельноп точкой L (в рассматриваемом случае ф({„) = , {tn) = г ири любом п). Л) Траектория, стремящаяся к состоянию равновесия (как в случае узла и фокуса, так и в случае седла), имеет своей едпп-ствепноп предельной точкой это состояние равновесия. 4) Для иолутраектории (или L~), имеющей вид спирали, наматывающейся па предельный цикл, очевидно, все точки этого предельного цикла являются предельными (в двух последних примерах предельная точка не являлась точкой соответствующей полутраектории). Так как сказанное относительно положительных полутраек-торпй, очевидно, справедливо и для отрицательных иолутраектории (с заменой t на -t), то в дальнейшем будут рассматриваться только положительные полутраектории. Следующая теорема позволяет ввести понятие предельной траектории. Теорема 1 (о предельной траектории). Если М*(1,*, г*) есть предельная точка полутраектории L, то и все точки траектории Lo, проходящей через точку М*, являются предельными для L+. Доказательство этой теоремы опирается па теорему о непрерывной зависимости от начальных условий и понятие предельной точки полутраектории. Траектория Lo называется предельной траекторией для полутраектории или просто предельной траекторией. Когда предельная точка траектории L является точкой самой этой траектории, то L называется самопределъной траекторией. В силу предыдущего состояние равновесия и замкнутая траектория являются самолредельными. В формулировке следующей теоремы используются теоретпко-мпожественпые понятия замкнутости и связности множества. [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [ 14 ] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] 0.0095 |