
 |
|
Главная страница Приемы качественного исследования [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [ 37 ] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] 2) неустойчивый узел при А > 2. Для исследования экватора сферы Пуанкаре полагаем X = 1/z, у = u/z. Получаем систему • -г(1-Ли + 0-Ли Z = - иг, U =-i----. (10) Полагая z = v, получаем v{i-hu + u) + hu Особая точка (z = 0, u = 0)-типа, исследованного в § 2 гл. 4. Имеем у = ф(и) = -Ан, t)(и) = 2Л2и + ... Проводя дополнительные рассмотрения, полностью аналогичные проведенному в предыдущем примере, можно показать, что особая точка имеет характер седла. Возвращаясь затем к системе 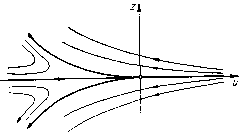 Рис. 73 (10) и устанавливая направления на траекториях, мы получаем картину, представленную на рис. 73. Для исследования «концов оси у» полагаем X = wjz, у = 1/z, получаем полагая z = v, получаем dv 2v {w - h) + 2hw\ dw „{i hw- w) + hw Это - также особая точка типа, исследованного в § 2 гл. 4. Имеем Pw (w, Ф (w)) + Qr, (w, Ф (w)) = 5hw + ... Это подходит под случай в) в теореме 4 гл. 4 - состояние равновесия имеет характер узла (рис. 74). Вид полусферы изображен 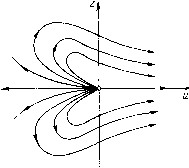 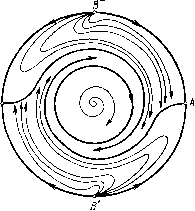 Рис. 74 Рис. 75 иа рис. 75. Очевидно, в силу расположения траекторий существует хотя бы один предельный цикл (на рисунке изображен только один). § 4. Критерии Бендиксона и Дюлака отсутствия предельных циклов. 1. Критерий Бендиксона. Если в некоторой односвязной области выражение Рх + Qy не меняет знака и не равно нулю тождественно, то в этой области не существует замкнутых контуров, составленных из траекторий. 2. Критерий Дюлака. Пусть В{х, у)-некоторая однозначная и дифференцируемая функция, и пусть D-IB {X, у) Р (X, у)] + [5 {X, y)-\-Q {X, у)] не меняет знака и не равно нулю тождественно в области G, ограниченной произвольными дугами {не траекториями и не дугами В{х, y)=0). Тогда: 1) Если G - односвязная область, то в области G не существует замкнутых контуров, составленных из траекторий {нет предельных циклов).
2) Если G - дву связная кольцевая область, то в области G не может быть более одного замкнутого контура, составленного из траекторий (более одного предельного цикла). Задача будет решена, если удастся подобрать В{х, у) таким образом, чтобы кривая D = 0 не имела действительных ветвей в тех областях плоскости (х, у), в которых можно ожидать наличия предельных циклов. Для разыскания функции В{х, у) не суш;ествует, однако, регулярных приемов. Пример 1. dy - д -f- gy -f- Q dx - у ~T Px + Qy= «• Если a 0, TO не существует замкнутых контуров, составленных из траекторий. Пример 2 [31]. dxfdt = у=Р, dy/dt =ax + by + а£- + Ру = Q. В качестве множителя В (ж, у)" возьмем функцию В (ж, i/) = e"2. Тогда не меняет знака в плоскости (ж, у) и не обращается тождественно в нуль, если ЪФО. Поэтому при любых значениях параметров (но 6=50) не существует замкнутых контуров, составленных из траекторий. Если 6 = 0, то В (ж, i/) = e~2* есть интегрирующий множитель. На плоскости (х, у) существует область, целиком заполненная замкнутыми фазовыми траекториями, охватывающими состояние равновесия типа центр. Пример 3 [37]. dx/dt=х{а(ю + аюх + aoiy) = Р{х, у), dy/dt = у{Ъоо + Ъ\ах -Ь 6oiy) = Q {х, у). Возьмем в качестве множителя В функцию В{х, у)==х-у-\ к- У(о-%) . °ioKi + V) д - д Тогда и, следовательно, D может обратиться в нуль только вдоль интегральных кривых ж = О и у = 0. Поэтому при о 6ooaio(aoi - 6oi)4- aoo6oi (6oi - аю) О в конечной части плоскости не существует замкнутых контуров, [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [ 37 ] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] 0.0133 |